Varianta 48

Prof: Ciocănaru Viorica

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului 20 + 100 : 25 este egal cu ….

(5p)     2. În intervalul (-1, 2] sunt …. numere întregi.

(5p)     3. Aria unui trapez cu linia mijlocie de 12 cm este de 108 cm². Înălţimea sa are … cm.

(5p)     4. Un kilogram de portocale costă 2,7 lei şi o ciocolată costă 3,2 lei. Pentru două kilograme de portocale şi trei ciocolate un copil plăteşte ….. lei.

(5p)     5. Un triunghi echilateral are înălţimea de 12 cm. Latura sa este de … cm.

(5p)     6. Un paralelipiped dreptunghic are dimensiunile de 4 cm, 10 cm, 6 cm. Aria sa totală este … cm².

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)    1. Desenaţi, pe foaia de examen, un cub ABCDA’B’C’D’ şi duceţi diagonalele AC’ şi AD’; precizaţi ce fel de diagonale sunt.

(5p)    2. Două cutii cu bomboane şi cinci prăjituri costă 35,9 lei iar trei cutii de bomboane şi două prăjituri de acelaşi fel costă 34,4 lei. Câţi lei costă o cutie de bomboane? Dar o prăjitură?

(5p)    3. Aflaţi perechile de numere întregi (a, b) pentru care are loc egalitatea (a+1)(b-1) =3.

 4. Fie funcţia f: R \(\to \)R, f(x) = -2x +3

(5p)    a). Reprezentaţi grafic funcţia f.

(5p)    b). Dacă se notează cu A şi B punctele de intersecţie ale graficului funcţiei f cu axele Ox şi Oy, determinaţi aria triunghiului AOB unde O este originea sistemului de coordonate.

(5p)     5. Se consideră numerele reale a = \({{\sqrt{{{(1+\sqrt{2})}^{2}}}}^{{}}}\)+ \({{\sqrt{{{(1-\sqrt{2})}^{2}}}}^{{}}}\)şi b =\(\sqrt{2}\). Calculaţi media geometrică a numerelor a şi b.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

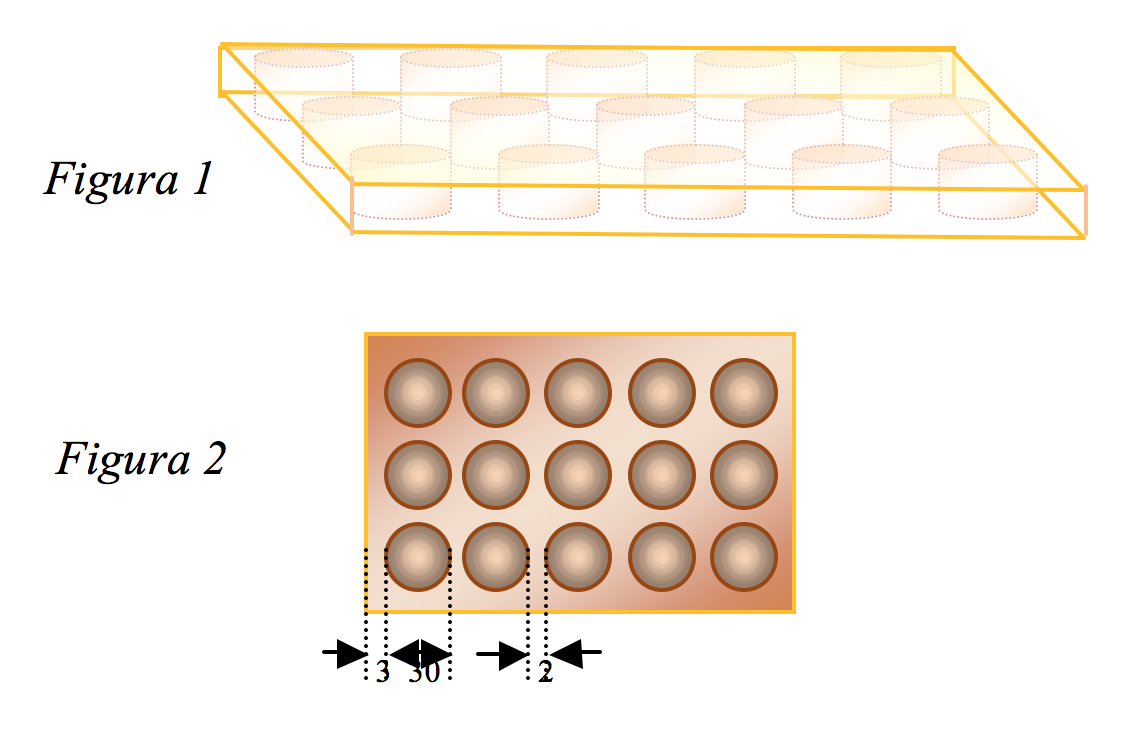
1. 1. Cutiile cu bomboane fine au suporturi cu alveole având forme asemănătoare cu cele ale bomboanelor. Un suport are 15 alveole cilindrice situate câte 5 pe un rând cu diametrul de 3 cm şi înălţimea de  2 cm.

 (5p)  a) Care este volumul alveolelor dintr-un suport? (Figura 1)

 (5p)  b) Care este aria părţii superioare a suportului bomboanelor dacă distanţa dintre alveole este de 2 mm şi până la marginile suportului, de la fiecare alveolă, sunt 3 mm? (Figura 2)

 (5p)  c) Dacă bomboanele au baza pătratică precizaţi suprafaţa maximă pe care se pot aşeza  în cele 15 alveole.

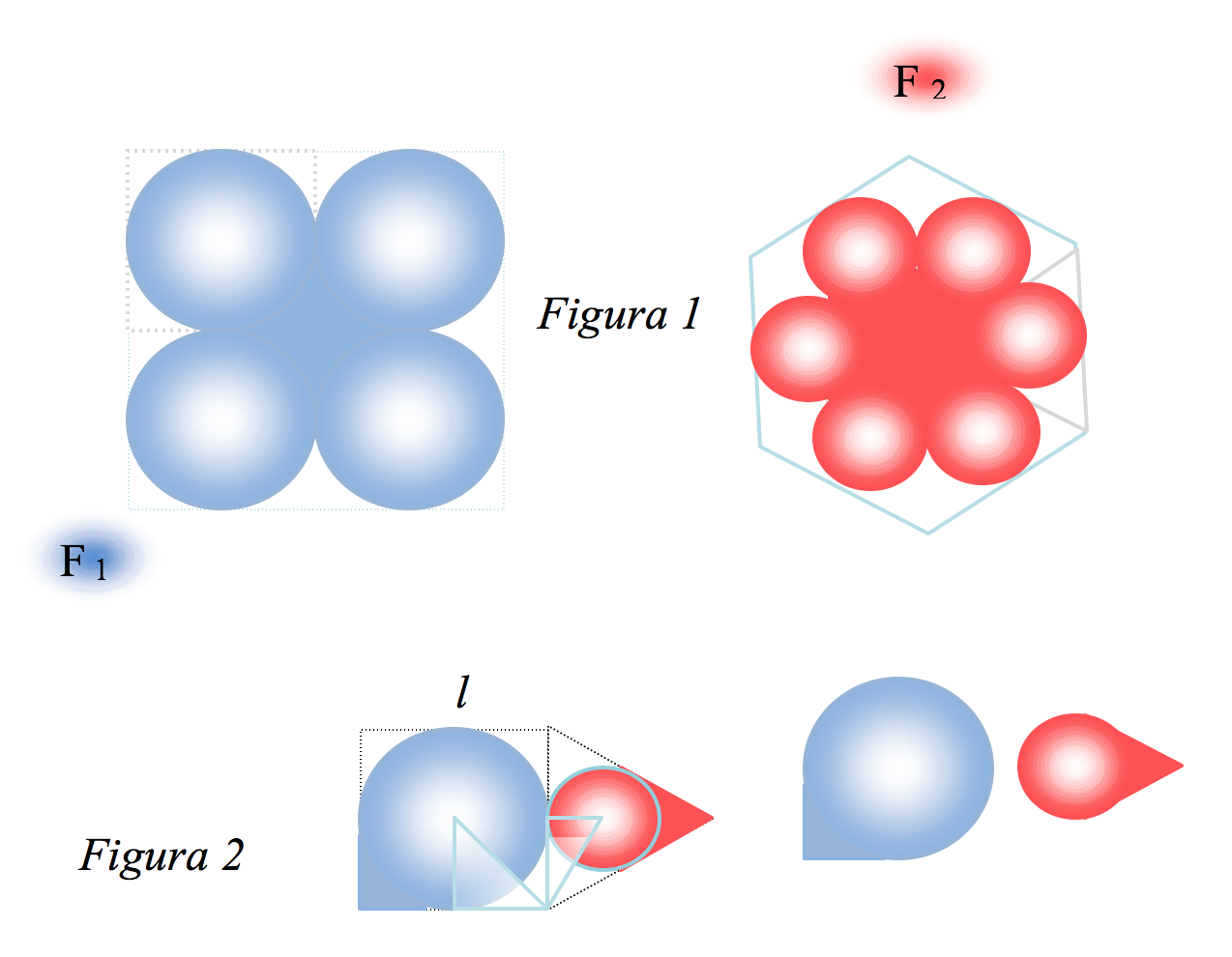
2. Elevii unei clase au confecţionat mărţişoare reprezentând flori (Figura 1). Pentru fiecare petală s-au folosit materiale sub formă de pătrat, respectiv triunghi echilateral cu laturile de aceeaşi lungime (Figura 2).

(5p)  a). Care este aria unei petale decupate din pătrat (A_petală1)?

(5p)  b). Care este aria unei petale decupate din triunghi echilateral (A_petală2)?

(5p)  c). Care este raportul ariilor celor două flori decupate din pătrat respectiv hexagon regulat  \(\frac{{{A}_{F1}}}{{{A}_{F2}}}\)?