Varianta 49

Prof: Ciocănaru Viorica

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(-\frac{1}{2}-(-\frac{3}{7})\frac{7}{5}\) este ….

(5p)     2. Ana a avut la ea suma de 75 de lei. După ce a cheltuit 48% din sumă, mai are … lei.

(5p)     3. Lungimile diagonalelor unui romb sunt 16 cm şi 40 cm. Aria rombului este egală cu … cm².

(5p)     4. Numărul 4 este soluţie a ecuaţiei 3x + a = 1 dacă a este …

(5p)     5. Aria unui pătrat este egală cu 64 cm². Perimetrul acestuia este egal cu … cm.

(5p)     6. Volumul unui cub este de 125 cm³. Lungimea diagonalei cubului este de … cm.

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, o piramidă patrulateră regulată VABCD. Desenaţi şi notaţi triunghiul format din înălţimea piramidei, apotema bazei şi apotema piramidei.

(5p)     2. Calculaţi expresia \({{(2x-\sqrt{3})}^{3}}\)pentru  x = \(\sqrt{2}\).

(5p)     3. Rezolvaţi, în R- {-3}, ecuaţia \(\frac{x-2}{x+3}=2\) şi precizaţi dacă soluţia găsită poate fi lungimea unui segment argumentând răspunsul.

 4. În sistemul cartezian xOy fie punctele A(2, 4) şi B(-1, -3).

(5p)    a) Determinaţi funcţia de gradul I, f: R \(\to \)R al cărei grafic conţine punctele A şi B.

(5p)    b) Reprezentaţi grafic funcţia f şi determinaţi coordonatele punctului C aflat la intersecţia perpendicularei din A pe Ox cu perpendiculara din B pe Oy, figurând punctual C în sistemul cartezian xOy.

(5p)     5. Rezolvaţi în mulţimea numerelelor reale ecuaţia \(\left| \left| x+2\sqrt{2} \right|-\sqrt{3} \right|\)= \(\sqrt{2}\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

   1. Pronaosul unei biserici este despărţit de naos prin două coloane de susţinere care au în secţiune forma din Figura 1. Latura triunghiului echilateral mare este de 60 cm iar latura fiecărui triunghi echilateral mic este de 20 cm. Coloanele, acoperite cu picturi, sunt înalte de 8 m.

 (5p)  a). Calculaţi suprafaţa pictată a coloanelor.

 (5p)  b). Determinaţi raportul procentual dintre suprafaţa circulară şi suprafaţa plană a coloanelor.

 (5p)  c). Determinaţi volumul coloanelor.

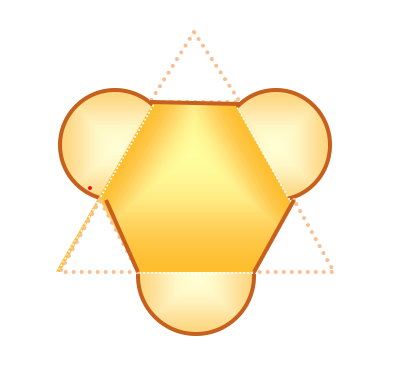                                         Figura 1

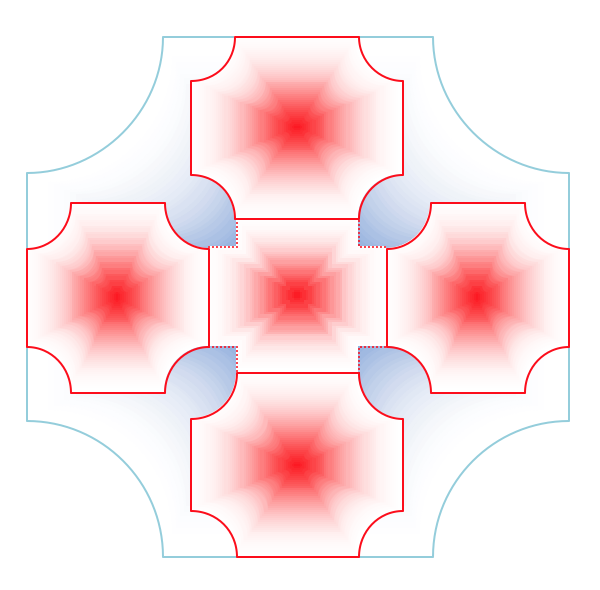
2. Un vitraliu cu motive geometrice are modelul din figură. Latura pătratului mare este de 60 cm, al celui mic de 20 cm. Raza sectorului de cerc mare este de 12 cm, a celui mic de 4 cm. Pătratul din centrul figurii are decupate colţurile sub formă de pătrăţele cu latura cât raza sectorului de cerc mic.

(5p)  a) Aflaţi lungimea conturului exterior (albastru) al vitraliului.

(5p)  b) Determinaţi lungimea conturului motivului geometric (roşu) al vitraliului (fiecare element se conturează şi la îmbinări).

(5p)  c) Determinaţi aria motivului geometric (roşu) al vitraliului.