Varianta 50

Prof: Ciocǎnaru Viorica

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului: 12 – 2 + 5² - 7 este ........

(5p)     2. Într-o clasǎ sunt 30 de elevi. Dacǎ numǎrul fetelor este 6, care este procentul bǎieţilor?

(5p)     3. Aria unui pǎtrat este de 64 cm². Fiecare diagonalǎ are lungimea de ..... cm.

(5p)     4. Pentru 2 kg de portocale şi o ciocolatǎ s-au plǎtit 9,2 lei iar pentru 4 kg de portocale şi 3 ciocolate s-au plǎtit 21,6 lei. Pentru 1 kg de portocale şi o ciocolatǎ se plǎtesc... lei.

(5p)     5. Dimensiunile unui paralelipiped dreptunghic sunt 8 cm, 6 cm, 24 cm. Diagonala sa are lungimea de ..... cm.

(5p)     6. Fie funcţia f : R \(\to \) R, f(x) = x – 2. Rezultatul calculului f (1) ∙ f (2) ∙ f (3) ∙ f (4) ∙.... ∙ f (n) este .....

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi pe foaia de examen tetraedrul PION cu baza ION şi vârful P.

(5p)     2. Fie a = \(\sqrt{8}-\frac{\sqrt{24}}{\sqrt{6}}\). Calculaţi a² şi a^-1.

(5p)     3. Pentru realizarea a 12 de minifelicitǎri s-au folosit 3 coli de hârtie şi 12 de plicuri timbrate. O coalǎ costǎ 0,6 lei iar un plic timbrat 1,3 lei. Cât costǎ minifelicitǎrile şi plicurile?

          4. Se considerǎ funcţiile f, g : R \(\to \) R, f(x) = 5x – 2 şi g(x) = - x + 4.

(5p)    a). Reprezentaţi grafic funcţiile f şi g în acelaşi sistem de coordonate.

(5p)    b). Determinaţi coordonatele punctului de intersecţie al graficelor celor douǎ funcţii.

(5p)     5. Rezolvaţi ecuaţia ||x – 2| - 5| = 3  unde x\(\in \)R.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

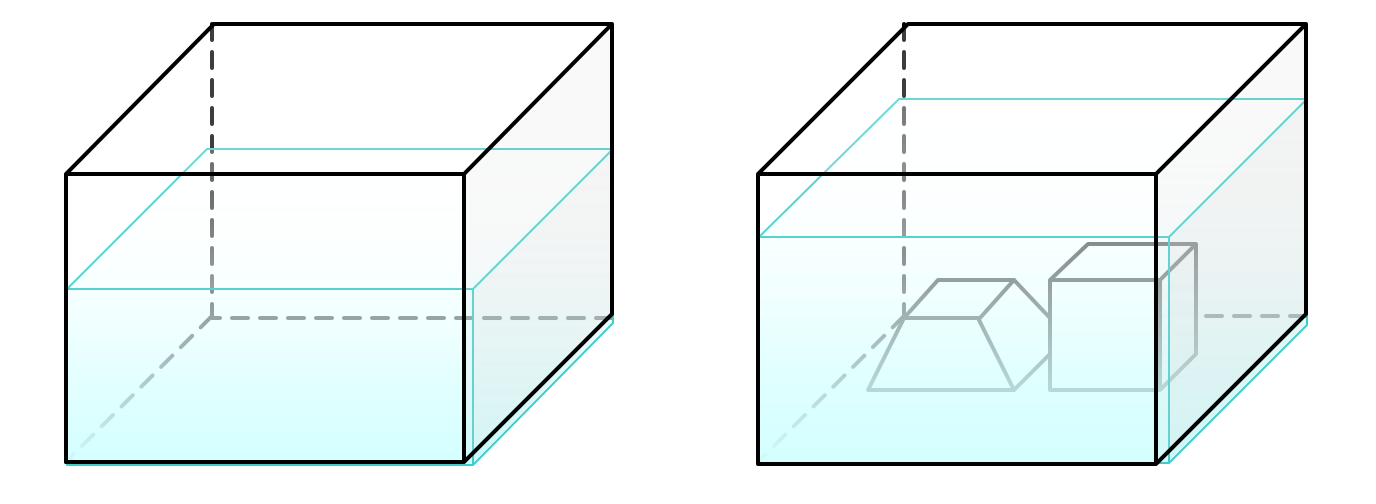
1. Într-un bazin cu apǎ sub formǎ de paralelipiped dreptunghic cu dimensiunile bazei de 20 m, 15 m şi înǎlţimea de 12 m, apa se ridicǎ pânǎ la 8 m înǎlţime. Se introduc în bazin douǎ corpuri pentru realizarea unor montaje; unul sub formǎ de trunchi de piramidǎ patrulaterǎ regulatǎ cu laturile bazelor de 6 m şi 3 m şi înǎlţimea de 4 m, celǎlalt sub formǎ cub cu muchia de 6 m.

(5p)  a).   Determinaţi volumul bazinului şi volumul apei din bazin.

 (5p)  b). Pânǎ la ce înǎlţime se ridicǎ apa în bazin dupǎ ce se introduc cele douǎ corpuri?

 (5p)  c). Ce procent reprezintǎ volumul trunchiului de piramidǎ din volumul apei? Dar al cubului din volumul bazinului?

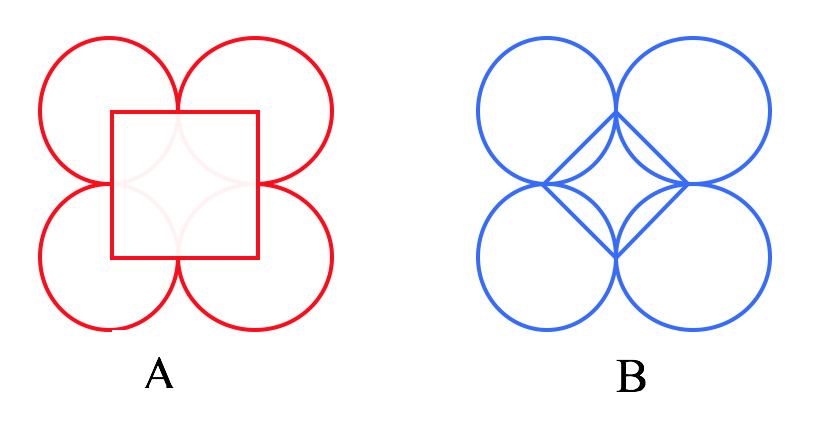
2. Un gard decorativ este confecţionat din elemente ca în figurile A şi B. Cercurile au razele egale cu R, iar pǎtratul din figura A are latura 2R; cel din figura B are latura R\(\sqrt{2}\).

(5p)  a). Cât material este necesar pentru 60 de elemente decorative din figura B?

(5p)  b). Cât material este necesar pentru 60 de elemente decorative din figura A?

(5p)  c). Dacǎ R = 3 cm aflaţi raportul lungimilor materialelor folosite în figura A respectiv B.