Varianta 51

Prof: Ciocǎnaru Viorica

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului \(\left( \frac{1}{2}-\frac{1}{3} \right)\cdot {{\left( \frac{2}{3} \right)}^{-1}}\) este egal cu ....

(5p)     2. Media geometricǎ a numerelor 3\(\sqrt{2}\) şi 12\(\sqrt{2}\) este egalǎ cu ....

(5p)     3. Fie f : R \(\to \) R, \(f(x)=3x-1\) şi M (a; -7)Î G_f. Atunci a este ....

(5p)     4. Aria unui dreptunghi cu lungimile laturilor  de x -2 şi x +2 este de 12 m². Diagonala dreptunghiului are lungimea de .... m.

(5p)     5. Suplementul complementului unui unghi cu mǎsura de 30⁰ este un unghi cu mǎsura de ....

(5p)     6. Un cub are muchia de 6 cm. Aria secţiunii diagonale este .... cm².

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi pe foaia de examen piramida SPORT, cu vârful S şi baza PORT cǎreia îi trasaţi diagonalele.

(5p)     2. Rezolvaţi în R inecuaţia: \(\frac{2x-1}{3}\) < \(\frac{3x+2}{2}\).

(5p)     3. Un obiect care costa 18 lei s-a ieftinit prima datǎ cu 15% iar a doua oarǎ cu 10%.Care este preţul sǎu dupǎ cele douǎ ieftiniri?

(5p)    4. Se considerǎ funcţia f : R \(\to \) R, f(x) = 2x +1 dacǎ  x < 0 sau -3x +1 dacǎ  x \(\ge \) 0

(5p)    a). Reprezentaţi grafic funcţia f.

(5p)    b)  Rezolvaţi ecuaţia: (2x +1)² = 2(- 3x + 1) în R.

(5p)     5. Plasaţi numǎrul a = \(\frac{{{(\sqrt{2}+\sqrt{3})}^{2}}}{(\sqrt{3}-1)(\sqrt{3}+1)}\) între doi întregi consecutivi.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. O cutie paralelipipedicǎ are dimensiunile bazei de 30 cm şi 20 cm, iar înalţimea de 40 cm. Feţele laterale şi capacul cutiei se acoperǎ cu vopsea.

 (5p)  a) Determinaţi ce suprafaţǎ se vopseşte.

 (5p)  b). Explicaţi dacǎ se poate introduce în cutie o baghetǎ cu lungimea de 50 cm.

 (5p)  c). În cutie se introduc cuburi cu muchia de 5 cm. Care este numǎrul maxim al acestora? Dar dacǎ muchia cubului este de 2 dm care este numǎrul maxim de cuburi?

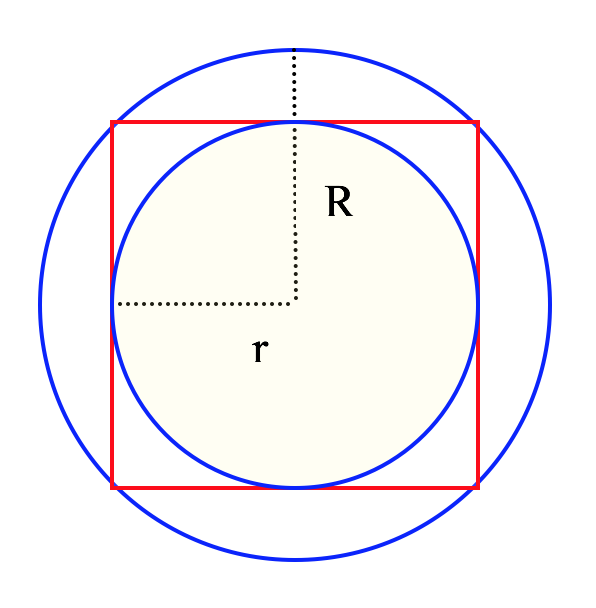
2. Un detaliu arhitectonic aratǎ ca în figura de mai jos. Latura pǎtratului este de 12 cm. Pǎtratul este înscris în cercul de razǎ R şi circumscris cercului de razǎ r.

(5p)  a). Aflaţi raportul \(\frac{r}{R}\).

(5p)  b). Determinaţi aria porţiunii cuprinse între pǎtrat şi cercul de razǎ r.

(5p)  c). Aflaţi raportul dintre perimetrul pǎtratului şi lungimea cercului de razǎ R.