Varianta 54

Prof: Cocalea Rodica

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(16-20:4\) este egal cu ....

(5p)     2. Într-o urnă sunt 10 bile numerotate de la 1 la 10. Se extrage o bilă. Probabilitatea ca    bila extrasă să fie numerotată cu un număr impar este ....  

(5p)     3. Trei kilograme de mere costă 8,25 lei. Cinci kilograme de mere de aceeaşi calitate costă ... lei.

(5p)     4. Un trapez cu bazele de 14 cm şi 10 cm are linia mijlocie de ... cm.

(5p)     5. O piramidă cu aria bazei de 24 cm² şi volumul de 120 cm³ are înălţimea egală cu ...      cm.

(5p)     6. În următorul tabel sunt trecute cantităţile de fructe existente la un moment dat într-    un depozit. Dacă în depozit sunt 2400 kg de fructe, atunci cantitatea de portocale este           egală cu …….kg.

SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, o prisma triunghiulară regulată cu bazele EXA,   respectiv MEN.

(5p)     2. Numerele reale a şi b sunt direct proporţionale cu numerele 3 şi 5. Calculaţi \(\frac{2a+3b}{a-2b}\).

(5p)     3. Un călător are de parcurs 291 km în trei zile. Ştiind că în a treia zi a parcurs cât media aritmetică a celorlalte zile, să se calculeze cât a parcurs în a treia zi.

 4. Fie funcţia \(f:R\to R,f(x)=-x+3\).

(5p)    a) Reprezentaţi grafic funcţia \(f\).

(5p)    b) Calculaţi \(P=f(-2012)\cdot f(-2011)\cdot f(-2010)\cdot ...\cdot f(2010)\cdot f(2011)\cdot f(2012)\).

(5p)     5. Dacă \({{a}^{2}}-{{b}^{2}}=12\)  şi \(a-b=2\), atunci calculaţi\(2{{(a+b)}^{2}}-3a+7+3(b-2)\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

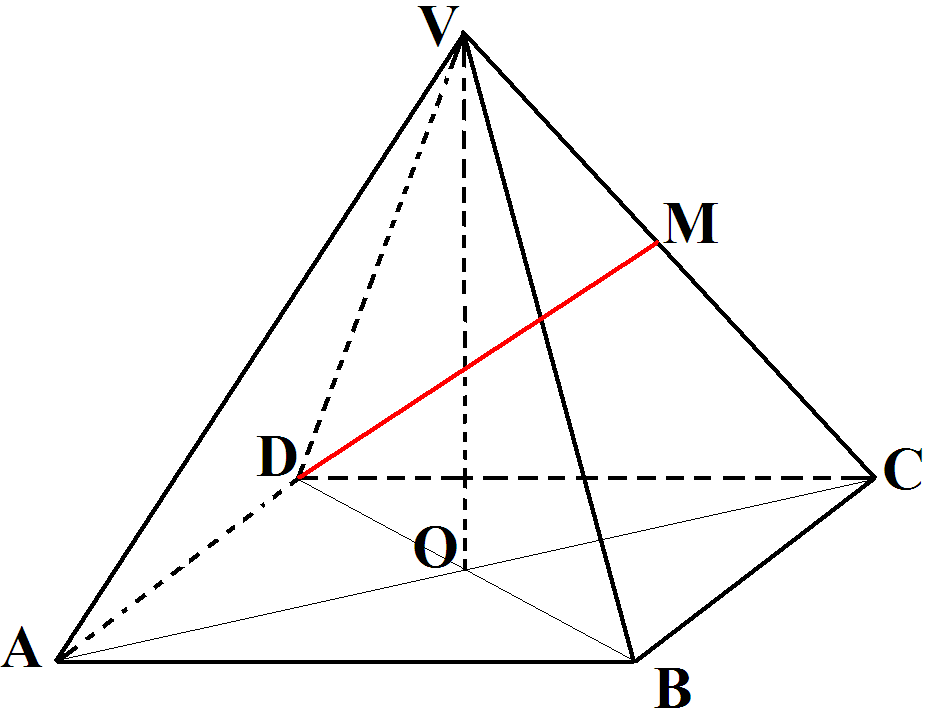
1. Piramida patrulateră regulată VABCD are dimensiunile \(AB=12\)dm şi triunghiul VAC dreptunghi isoscel.

 (5p)  a) Calculaţi aria laterală a piramidei.

 (5p)  b) Să se calculeze unghiului format de dreapta DM şi planul (ABC), unde M este mijlocul muchiei [VC]. 

(5p)  c) Dacă piramida se umple cu apă, să se verifice dacă încap 410 litri de apă. (\(1,41<\sqrt{2}<1,42\))

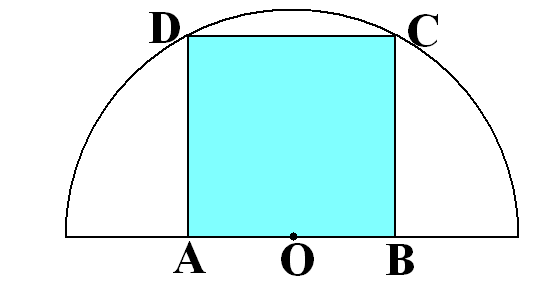
 2. Un rond de flori are forma unui semicerc ca în figura alăturată. Grădinarul vrea să planteze lalele în pătratul ABCD, iar restul rondului să fie plantate panseluţe. Raza cercului din care provine semicercul este egală cu \(2\sqrt{5}\)m.

(5p)  a) Aflaţi aria semicercului.

 (5p)  b) Aflaţi lungimea laturii terenului plantat cu lalele.

 (5p)  c) Arătaţi că suprafaţa plantată cu lalele este mai mare decât cea plantată cu panseluţe, ştiind că  \(3,14<\pi <3,15\).