Varianta 56

Prof: Cocalea Rodica

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(36-0,6\cdot 10\) este egal cu ....………………….

(5p)     2. Un muncitor pune parchetul într-un apartament în şase zile. Dacă ar lucra doi   muncitori, atunci ar pune parchetul în acelaşi apartament în ... zile.

(5p)     3. Trei kilograme de roşii şi două kilograme de castraveţi costă 6,50 lei. Şase kilograme de roşii şi patru kilograme de castraveţi de aceeaşi calitate costă ... lei .

(5p)     4. Diametrul unui cerc este de 16 cm, atunci lungimea cercului este egală cu ... cm.

(5p)     5. O piramidă triunghiulară regulată VABC are VA = AB = 8 cm. Suma tuturor muchiilor piramidei este egală cu ... cm.

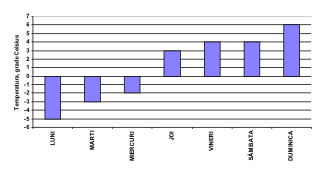
(5p)     6. În diagramă este reprezentată evoluţia temperaturilor înregistrate la ora 20 pe parcursul unei săptămâni. Diferenţa dintre temperatura cea mai mare şi cea mai mică este egală cu ….°C.

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, un cub şi notaţi-l cu ABCDA'B'C'D'.

(5p)     2. Dacă a şi b sunt numere reale care verifică relaţia\(4a-3b-6=0\), atunci calculaţi \({{(11-8a+6b)}^{2012}}\).

(5p)     3. Un bunic împarte la nepoţi câte 5 bomboane şi constată că îi mai rămân în pungă 3      bomboane. Dacă încearcă să împartă câte 6 bomboane, rămân 4 nepoti numai cu câte 5 bomboane. Determinaţi câţi nepoţi are bunicul.

4. Fie funcţia \(f:R\to R,f(x)=\frac{1}{2}x-3\).

(5p)    a) Reprezentaţi grafic funcţia \(f\).

(5p)    b) Determinaţi coordonatele punctului de pe grafic care are abscisa egală cu opusul ordonatei şi aparţine graficului funcţiei.

(5p)     5. Simplificaţi raportul  \(\frac{{{x}^{2}}+x-12}{{{x}^{2}}-6x+9}\) cu \(x-3\), unde \(x\in R\backslash \{3\}\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Un rezervor are forma unui paralelipiped dreptunghic cu dimensiunile de 2,4 m, 3,6 m, iar înălţimea de 4 m. O piramidă patrulateră regulată cu toate muchiile egale cu 2 m se scufundă în bazin.

 (5p)  a) Fundul bazinului este pavat cu plăci de gresie dreptughiulară cu lungimea de 30 cm      şi lăţimea de 20 cm. Câte plăci de gresie au fost folosite pentru a acoperi tot fundul      bazinului?

 (5p)  b) Calculaţi volumul unei piramide cu toate muchiile egale cu 2 m.

 (5p)  c) Bazinul este umplut mai mult de jumătate cu apă. Dacă se scufundă piramida în bazin, cu câţi centimetrii se va ridica apa în rezervor?

 2. Un teren agricol are forma unui trapez isoscel ABCD cu baza mare AB = 40 m şi baza mică CD = 30 m, iar măsura unghiului obtuz de 120⁰.

(5p)  a) Calculaţi suprafaţa terenului.

(5p)  b) Suptafaţa triunghiulară ADC se cultivă cu fasole, iar restul terenului se cultivă cu roşii. Cu câţi metri pătraţi este mai mare suptafaţa cultivată cu roşii faţă de cea cultivată cu fasole.

(5p)  c) Pentru a împrejmui terenul cu sârmă ghimpată se montează stâlpi, între doi stâlpi consecutivi fiind distanţa de 2,5 m. Câţi stâlpi sunt necesari pentru realizarea acestei lucrări?