Varianta 57

Prof: Constantin Corina

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(15-15:3\) este egal cu ...

(5p)     2. Într-o cutie sunt 4 figurine albe şi 5 roşii. Probabilitatea ca o figurină extrasă să fie roşie este egală cu ...

(5p)     3. Trei kilograme de portocale costă 6,60 lei. Treizeci de kilograme de portocale de aceeaşi calitate costă ... lei.

(5p)     4. Un pătrat cu aria de 169 cm², are latura de lungime ... cm.

(5p)     5. În Figura 1 este reprezentat un paralelipiped dreptunghic ABCDA’B’C’D’. Dacă aria laterală a paralelipipedului este egală cu 78 cm² şi înălţimea cu 3 cm, atunci perimetrul bazei este egal cu ... cm.

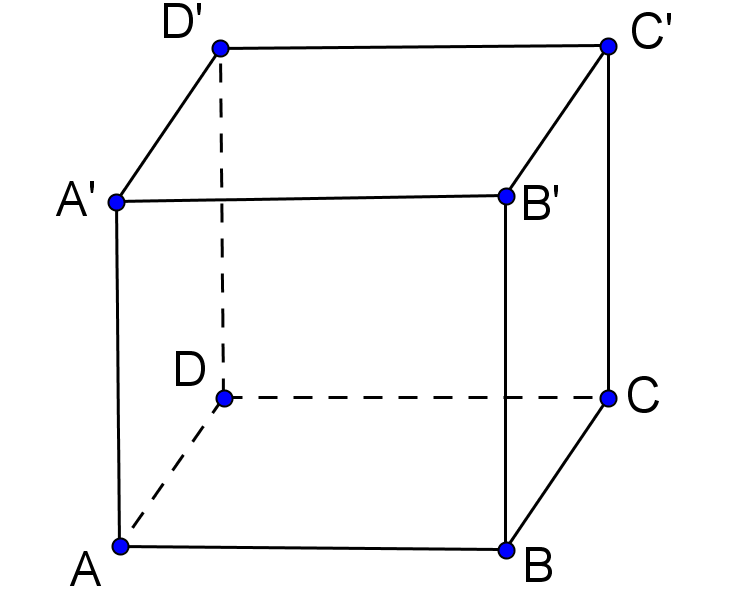Figura 1

(5p)     6. În tabelul de mai jos sunt prezentate, în procente, rezultatele unui număr de 25 elevi la un concurs de matematică.

Numărul elevilor care au obţinut o notă cel puţin egală cu 7 este ...

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, o piramidă patrulateră regulată VABCD.

(5p)     2. Aflaţi elementele mulţimii \(A=\left\{ x\in \mathbb{Z}\left| \frac{3}{2x-1}\in \mathbb{Z} \right. \right\}\).

(5p)     3. Numerele 1507, 364 şi 458 împărţite la acelaşi număr natural x dau respectiv resturile 7, 4 şi 8. Determinaţi numărul x.

4. Fie funcţia \(f:\left\{ -1,1,3 \right\}\to \mathbb{R}\), \(f\left( x \right)=3x+2\).

(5p)    a) Determinaţi mulţimea valorilor funcţiei.

(5p)    b) Rezolvaţi inecuaţia \(\left| f\left( x \right) \right|\le 1\).

(5p)     5. Verificaţi identitatea \({{\left( x-1 \right)}^{2}}+\left( x+3 \right)\left( x-3 \right)-{{\left( x+2 \right)}^{2}}={{\left( x-3 \right)}^{2}}-21\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Pe un teren de formă dreptunghiulară cu dimensiunile AB = 6 m şi BC = 8 m, se ridică doi stâlpi [AM] şi [DN] de lungimi AM = 4 m şi DN = 2 m, ca în Figura 2.

 (5p)  a) Arătaţi că BC ǁ (AMN).

 (5p)  b) Aflaţi distanţa de la punctul M la segmentul [BD].

 (5p)  c) O rândunică situată în punctul M zboară până în punctul N, după care îşi continuă drumul coliniar cu M şi N, până atinge pământul în punctul P. De aici zboară razant până în punctul C, unde a zărit un viermişor. Calculaţi lungimea drumului parcurs de rândunică şi rotunjiţi la cifra unităţilor.

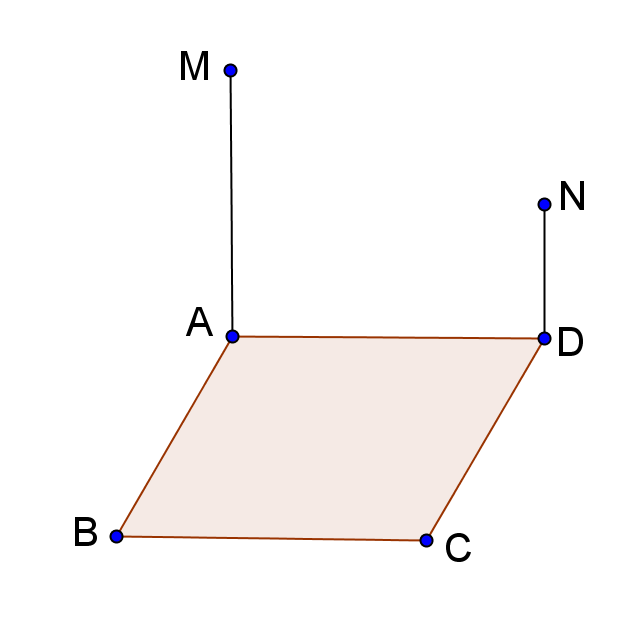Figura 2

 2. O fântână arteziană, situată pe un disc, are o bordură în formă de coroană circulară, pe care se plantează gazon, ca în Figura 3. Lungimea cercului interior este de \(4\pi \)m, iar a cercului exterior de \(10\pi \)m.

(5p)  a) Aflaţi raza discului pe care se află fântâna.

(5p)  b) Aflaţi lăţimea bordurii cu gazon.

(5p)  c) Cât costă gazonul plantat, dacă pentru 20 m² de gazon se utilizează 1 kg de gazon, iar preţul unui kilogram de gazon este de 25 lei? (\(\pi \simeq 3,14\))

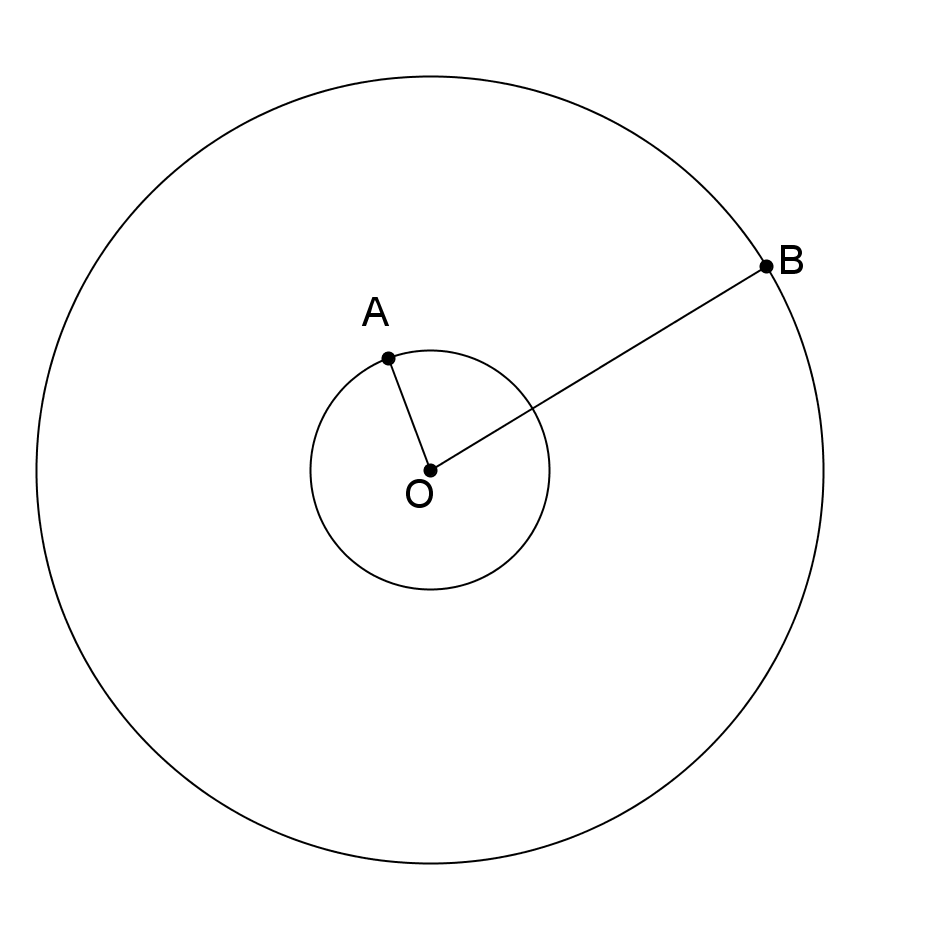Figura 3