Varianta 58

Prof: Constantin Corina

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(7+7\cdot 5\) este egal cu ...

(5p)     2. Numerele naturale din intervalul [-7, 1] sunt ...

(5p)     3. Opt lucrători muncesc pe un şantier 8 ore pentru a termina o parte dintr-o lucrare. 16 lucrători vor munci ... ore pentru a termina aceeaşi parte din lucrare.

(5p)     4. Un romb cu diagonala mică de 7 cm şi diagonala mare triplul diagonalei mici are aria egală cu ... cm².

(5p)     5. În Figura 1 este reprezentată o prismă patrulateră regulată dreaptă ABCDA’B’C’D’, cu feţele laterale pătrate. Dacă muchia bazei are lungimea de 8 cm, atunci volumul prismei este egal cu … cm³.

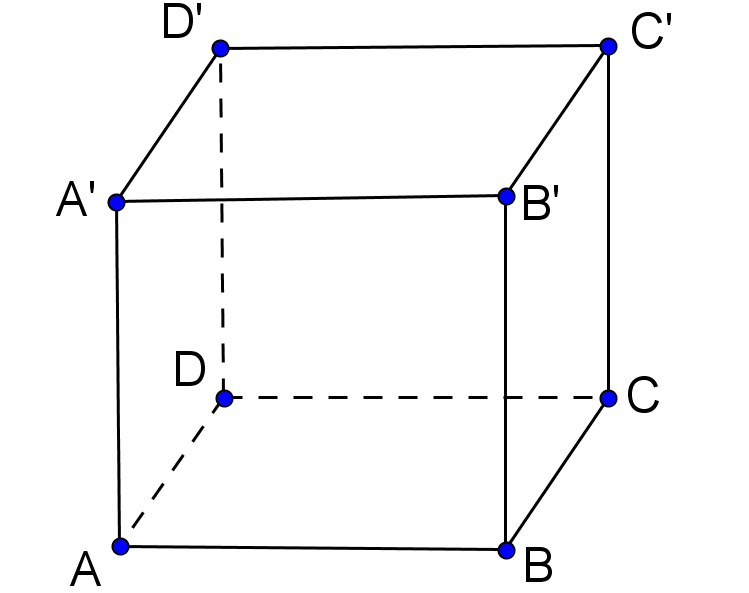
Figura 1

(5p)     6. În Figura 2 este prezentată, printr-o diagramă circulară, repartizarea terenului cu diverse culturi. Porţiunile haşurate au suprafeţe egale. Una dintre cele două suprafeţe haşurate reprezintă ... %.

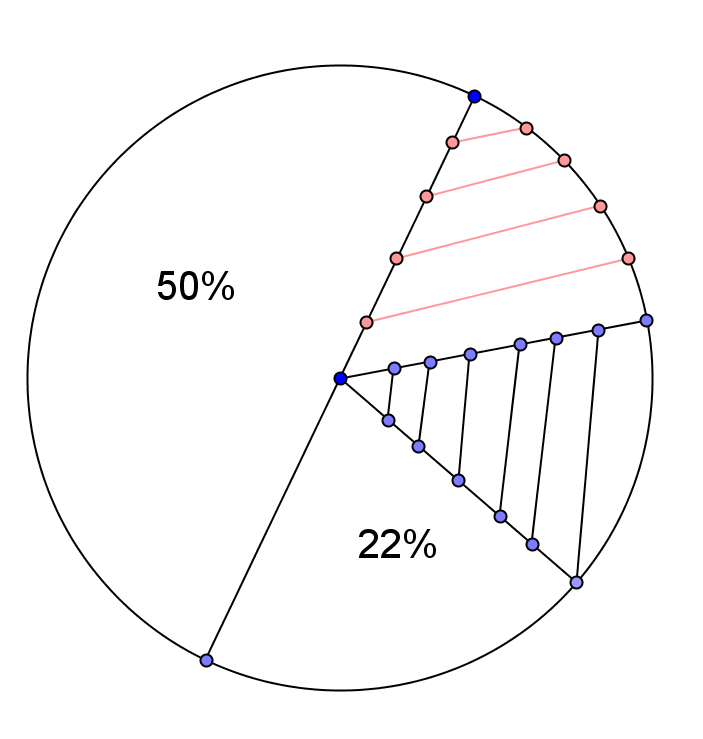
Figura 2

SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, o piramidă triunghiulară regulată VABC.

(5p)     2. Aflaţi numărul a natural, dacă \(\left( a-1 \right)\left( a+3 \right)=5\).

(5p)     3. Preţul unui televizor este de 992 lei, preţ în care este inclus TVA-ul de 24%. Aflaţi cât reprezintă TVA-ul în lei.

 4. Fie funcţia \(f:\mathbb{R}\to \mathbb{R}\), \(f\left( x \right)=x-5\).

(5p)    a) Reprezentaţi grafic funcţia.

(5p)    b) Determinaţi măsura unghiului determinat de graficul funcţiei şi axa absciselor.

(5p)     5. Arătaţi că numărul \(\sqrt{19+8\sqrt{3}}-\left| 2\sqrt{3}-1 \right|+\sqrt{3}\) este natural.

SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Pe un teren se construieşte o piramidă patrulateră regulată, cu muchia bazei de 6 m şi muchia laterală de 5m. Piramida este confecţionată din sticlă.

 (5p)  a) Arătaţi că apotema piramidei este de 4 m.

 (5p)  b) Câţi m² de sticlă sunt necesari pentru confecţionarea piramidei?

 (5p)  c) Aflaţi drumul minim parcurs de o furnică pe suprafaţa laterală a piramidei, dacă ea pleacă din punctul B şi ajunge în punctul D.

 2. Figura 3 reprezintă schiţa unei grădini dreptunghiulare, în care sunt plantate flori în 3 ronduri sub formă de discuri. Zonele în care se află rondurile sunt separate de 2 alei pavate cu pietriş. Rondul mare este tangent celor 2 alei. În jurul rondurilor se află gazon. Datele se află în figură.

(5p)  a) Calculaţi suprafaţa destinată florilor.

(5p)  b) Arătaţi că suprafaţa cu gazon este mai mică decât 54 m² (\(3,14<\pi <3,15\)).

(5p)  c) O furnică merge în linie dreaptă, mai întâi din punctul A în punctul O, apoi din punctul O în punctul B. Punctul O se află la mijlocul lăţimii grădinii. Calculaţi distanţa parcursă de furnică, rotunjită la cifra zecimilor.         

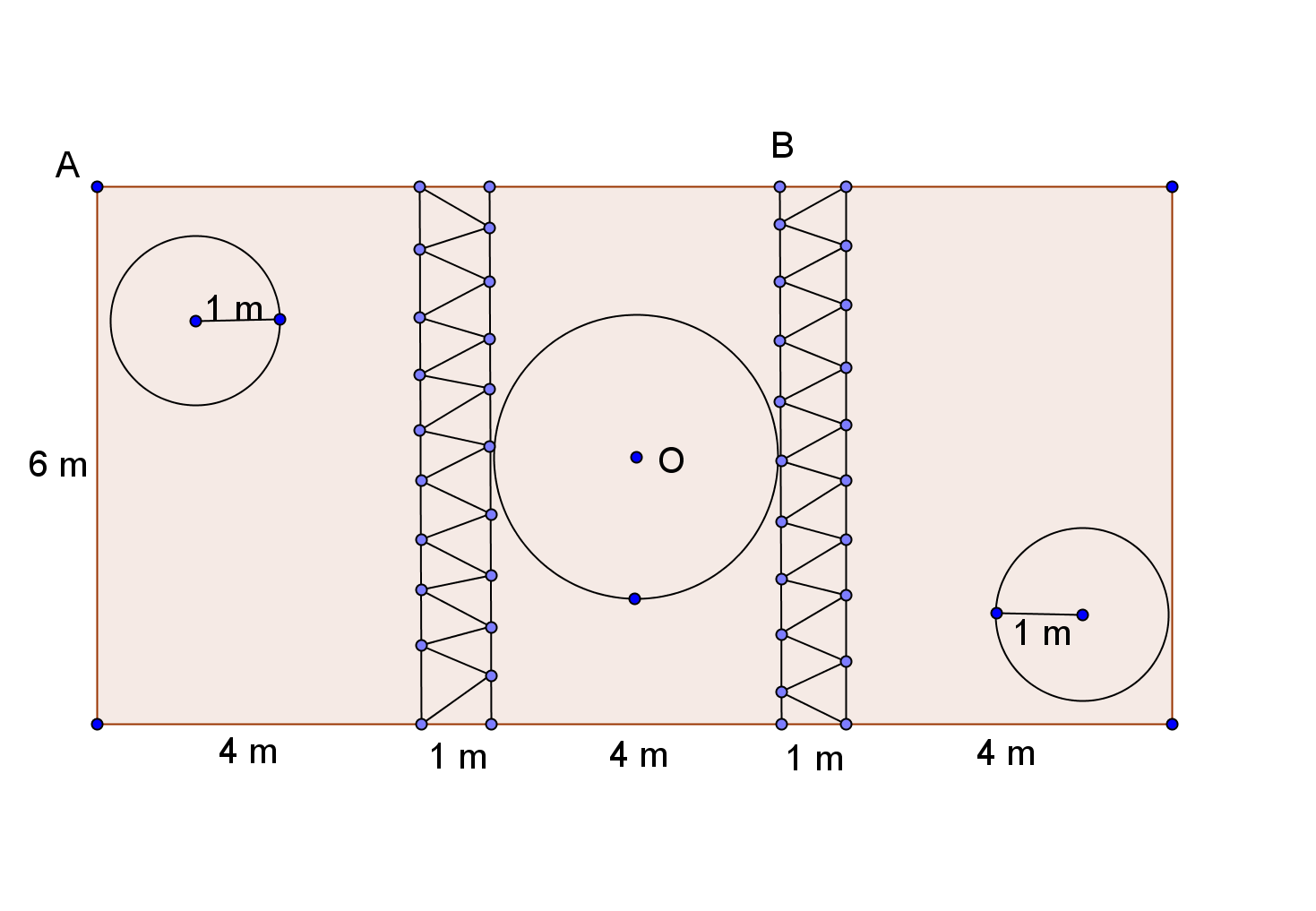
Figura 3