Varianta 59

Prof: Constantin Corina

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(8:8+6\) este egal cu ...

(5p)     2. Numerele din mulţimea \({{\mathbb{Z}}^{*}}\cap \left\{ -1,0,1 \right\}\) sunt în număr de ...

(5p)     3. Numărul x din proporţia \(\frac{x}{7}=\frac{16}{14}\) are valoarea ...

(5p)     4. Un trapez cu aria de 144 cm² şi înălţimea de 9 cm, are linia mijlocie de lungime ... cm.

(5p)     5. În Figura 1 este reprezentat un tetraedru regulat VABC. Dacă aria totală a tetraedrului este egală cu \(25\sqrt{3}\)cm², atunci muchia are lungimea de ... cm.

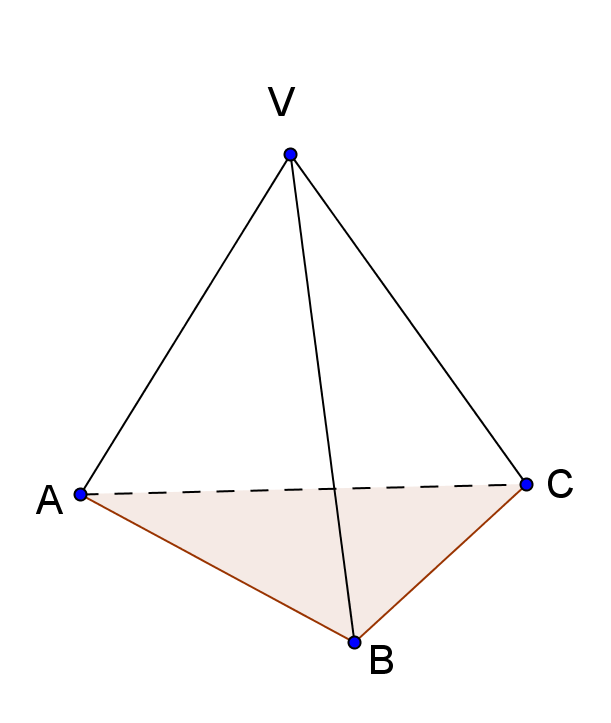
Figura 1

(5p)     6. Un număr de 200 elevi sunt chestionaţi în legătură cu numărul orelor petrecute pe calculator într-o săptămână (1 săptămână = 7 zile). Situaţia este prezentată în tabelul de mai jos.

Numărul elevilor care petrec cel mult 2 ore pe zi pe calculator este egal cu ...

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, un cub ABCDA’B’C’D’.

(5p)     2. Determinaţi elementele mulţimii \(B=\left\{ x\in \mathbb{R}\left| \left| 5x+3 \right|\le 7 \right. \right\}\).

(5p)     3. Aflaţi toate numerele naturale cuprinse între 100 şi 200, care împărţite la 3, 5 şi 4 dau de fiecare dată restul 2 şi câturile nenule.

 4. Fie funcţia \(f:\mathbb{R}\to \mathbb{R}\), \(f\left( x \right)=2x-1\).

(5p)    a) Reprezentaţi grafic funcţia.

(5p)    b) Aflaţi aria triunghiului determinat de graficul funcţiei f, axa ordonatelor şi reprezentarea grafică a funcţiei \(g:\mathbb{R}\to \mathbb{R}\), \(g\left( x \right)=1\).

(5p)     5. Simplificaţi fracţia \(\frac{{{\left( {{x}^{2}}+x \right)}^{2}}-4}{\left( {{x}^{2}}+x \right)\left( {{x}^{2}}+x+1 \right)-6}\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. O cutie de carton ABCDA’B’C’D’ este umplută cu 3 straturi de cubuleţe roşii care au muchia de 3 cm.

 (5p)  a) Aflaţi volumul unui cubuleţ roşu.

 (5p)  b) Aflaţi dimensiunile cutiei de carton, dacă pe fiecare strat se aşează 20 cubuleţe pe lungime şi 10 pe lăţime, iar cutia de carton este umplută la maxim.

 (5p)  c) Determinaţi tangenta unghiului  dintre planul (ABC’) şi planul bazei, în condiţiile de la punctul b), lăţimea fiind BC, iar înălţimea BB’.

 2. Pentru pavarea unei străzi se folosesc 1000000 de pietre cubice cu muchia de 5 cm.

(5p)  a) Ce suprafaţă (în m²) se poate pava cu aceste pietre?

(5p)  b) Cât costă pavarea străzii, dacă la preţul pietrei se adaugă 10% manopera? Piatra costă 45 lei/ m².

(5p)  c) Dacă 1 m³ de piatră cântăreşte 2 tone, câte transporturi trebuie să facă un camion, dacă el poate transporta 15 tone?