Prof: Conţu Valentin

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Dacă  35 + 2x - 4 = 3x +32,5 , atunci numărul x este egal cu………..

(5p)     2. O echipă de muncitori ar putea termina o lucrare în 10 ore . Dacă muncitorii lucrează la fel, atunci un sfert din membrii echipei vor termina lucrarea în ………..ore.

(5p)     3 După o diminuare cu 25% un produs are valoarea de 1080 lei. Valoarea  iniţială era de……lei.

(5p)     4. Într-un triunghi dreptunghic raportul măsurilor unghiurilor ascuţite este de \(\frac{4}{5}\). Unghiul cel mai mic are măsura de…..

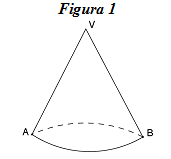
(5p)     5. Se consideră conul circular drept din Figura 1. Dacă aria laterală este de două ori mai mare decât aria bazei atunci măsura unghiului AVB este de ………⁰ 

(5p)     6. În  tabelul din figura 2  este ilustrată situaţia dintr-un bloc de locuinţe. Numărul total de camere  este egal cu………. 

SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi , pe foaia de examen, o prismă triunghiulară regulată şi notaţi varfurile bazelor cu literele  A,B,C şi D,E,F .

(5p)     2. consideră mulţimea \(A=\left\{ x\in R_{{}}^{{}}\text{/}_{{}}^{{}}\left| \frac{2x+3}{2} \right|\le 5 \right\}\) . Enumeraţi elementele mulţimii \(A\cap {{Z}_{-}}\)

(5p)     3. Un biciclist parcurge intr-o zi 0,(3) din lungimea unui traseu, a doua zi parcurge jumătate din distanta parcursă în prima zi iar în ziua a treia 120 km şi mai rămâne de parcurs un sfert din traseu. Care este lungimea traseului ?

 4. Se consideră funcţia \(f:R\to R\), unde \(f(x)=-2x+6\)

(5p)    a) Reprezentaţi graficul  funcţiei, într-un sistem de axe ortogonale.

(5p)    b) Determinaţi distanţa de la originea sistemului de axe până la cel mai apropiat punct de pe graficul funcţiei.

(5p)     5. Arătaţi că numărul \(n={{\left( 3-\frac{\sqrt{7}}{2} \right)}^{2}}+{{\left( 3+\frac{\sqrt{7}}{2} \right)}^{2}}+2\cdot \left( 3+\frac{\sqrt{7}}{2} \right)\cdot \left( 3-\frac{\sqrt{7}}{2} \right)\)    este  pătratul unui număr natural.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Un rezervor de tablă are forma de cilindru circular drept și are aria laterală egală cu suma ariilor bazelor . Se știe că aria  și perimetrul bazei sunt exprimate in metri pătrați , respectiv metri, prin același număr.

 (5p)  a) Determinați  lungimea razei bazei acestui rezervor.  

 (5p)  b) Cât cântăreste rezervorul dacă 1 metru părat de tablă are masa de 20 kg  ? ( se consideră \(\pi \cong 3,14\))

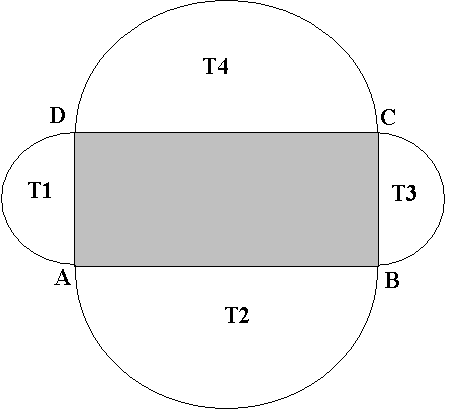
 (5p)  c) Dacă tabla din care  este confecționat  rezervorul  se livrează în role cu lungimea de 110 de metri și lățimea de 4 metri, iar pereții si bazele rezervorului se obțin prin decupare din rola de tabla fara lipirea bucaților de tablă rămase, determinați care este numărul maxim de rezervoare care pot fi realizate dintr-o rolă  ?2. O arenă are un teren de tenis ABCD în formă dreptunghiulară cu AB = 32 m

şi AD = 16 m. Tribunele T₁; T₂; T₃ şi  T₄ sunt semicercuri .

(5p)  a) Care este suprafaţa tribunelor ( se consideră \(\pi \cong 3,14\)) ?

(5p)  b) Verificaţi dacă suprafeţelor totală a tribunelor  este de două ori  mai mare decât   suprafaţa terenului ?

(5p)  c) Daca în interiorul complexului (terenul cu tribune) se monteză două camere de televiziune pentru supraveghere , aflaţi care este distanţa maximă dintre cele două camere .