Varianta 62

Prof: Conţu Valentin

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului  18– 3² este egal cu………..

(5p)     2. Numerele întregi din  intervalul ( – 4,5) sunt un număr de …… .

(5p)     3 O cantitate de miere încape în 12 borcane de 250 de grame . Dacă aceeaşi cantitate de miere va fi pusă în borcane de 300 grame , atunci numărul borcanelor de 300 grame va fi ……… 

(5p)     4. Lungimile laturilor unui paralelogram sunt exprimate prin numere întregi  consecutive , iar perimetrul paralelogramului este de 18 cm. Dacă paralelogramul are un unghi cu măsura de 60 ⁰ , atunci aria sa va fi de …….cm²  

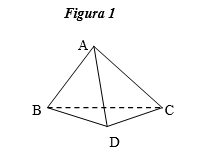
(5p)     5 În Figura 1  este reprezentat un tetraedru regulat ABCD. Dacă   aria totală a tetraedrului este egală cu \(9\sqrt{3}\) cm² , atunci muchia AC va avea lungimea de………..cm

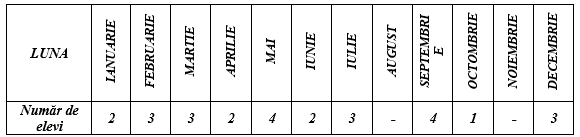
(5p)     6. Un copil a realizat următorul tabel  cu aniversările elevilor  din clasa sa

Numărul elevilor din clasă este egal cu…………..

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, o prismă patrulateră regulată şi notaţi vârfurile bazelor cu literele  A,B,C,D,A’,B’,C’,D’.

(5p)     2. Determinaţi suma numerelor reale  a ,b şi c , dacă a + 2b + 3c = 38 şi  6a + 4b + 2c   = 68

(5p)     3. Un tren international pleacă din Paris pe data de 30 decembrie 2011 ora 8 si 35 minute şi trebuie să ajungă la Bucureşti pe data de 1 ianuarie 2012 ora 20 si 20  minute. Dacă trenul are  o întârziere de 50 minute calculaţi durata călătoriei .

4. Se consideră funcţiile\(f:R\to R\) şi \(g:R\to R\), unde \(f(x)=-\frac{4}{3}x+8\) şi \(g(x)=4\)

(5p)    a) Reprezentaţi graficul  funcţiei  \(f\), într-un sistemul de axe ortogonale xOy.

(5p)    b) Calculaţi aria trapezului determinat de graficele celor două funcţii şi axele sistemului de coordonate.

(5p)     5. Arătaţi că numărul \(n=\sqrt{14-6\sqrt{5}}+\sqrt{9-4\sqrt{5}}\) este număr natural.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Un cub de gheaţă ale aria totală şi volumul exprimate în metri pătraţi prin acelaşi număr natural .

 (5p)  a) Arătaţi că  muchia cubului are lungimea de 6 metri ?   

 (5p)  b) Dacă densitatea  gheţii este de aproximativ 900 Kg/m³ ,calculaţi masa cubului de gheaţă exprimată în tone  .

 (5p)  c) Dacă apa provenită din cubul de gheaţă este colectată intr-un bazin în formă de paralelipiped dreptunghic  cu lungimea  de 12m şi lăţimea de 8,1 m şi se cunoaşte că densitatea apei este de 1000 Kg/m³, aflaţi  care este nivelul apei din bazin?

   Obs:  Masa unui corp este  produsul dintre volumul corpului şi densitatea substanţei corpului.

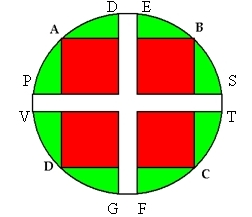
 2. Figura 2 reprezintă un parc care are formă de cerc cu raza de 50 de metri. Prin parc sunt două alei dreptunghiulare  care au  lăţimea de  4 metri .    

(5p)  a) Care este suprafaţa aleilor  ( se consideră ca aleile sunt dreptunghiuri cu lungimea egală cu diametrul cercului ) ?

(5p)  b) Dacă în pătratul ABCD sunt plantate câte 4 de trandafiri pe m² şi valoarea unui

 trandafir este de 12 lei  aflaţi numărul necesar de trandafiri şi preţul lor   ? (se exclude suprafaţa aleilor iar valoarea lui \(\sqrt{2}\)  pentru calculul suprefeţelor aleilor se consideră = 1,4)

(5p)  c) Dacă toată suprafaţa parcului a fost irigată cu apa depozitată într-un rezervor în formă de paralelipiped dreptunghic cu L= 20 m, l= 6 m şi h = 3,15 m şi că pentru un m² de teren din parc sunt necesari 2 litri de apă zilnic Aflaţi de câte ori a trebuit umplut bazinul dacă parcul a fost irigat în zilele fără precipitaţii  începând din  26 aprilie, până pe 31 august  inclusiv şi că tot în această perioadă au fost  20 de zile cu precipitaţii  ( \(\pi \)=3,15).

      Precizăm că bazinul trebuie umplut complet şi golit complet la fiecare umplere respectiv golire.