Varianta 63

Prof: Conţu Valentin

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

5p  1.  Opusul numărului \(-\frac{3}{5}\) este egal cu ……….

5p. 2. Media aritmetică a numerelor  \(a=3+\sqrt{2}\) şi \(b=1-\sqrt{2}\) este egală cu ……….

5p. 3. Mulţimea numerelor reale care satisfac relaţia  \(-5\le 2x-3\le 3\)   este intervalul ………

5p. 4. Dreptunghiul cu lungimea de 8 cm şi aria  egală cu 40 cm²  are perimetrul de ……….cm

5p. 5. Piramida regulată ROSIE are vârful R şi  feţele laterale triunghiuri echilaterale. Dacă latura bazei OS are lungimea de 6 cm atunci suma lungimilor tuturor muchiilor este de……….cm.

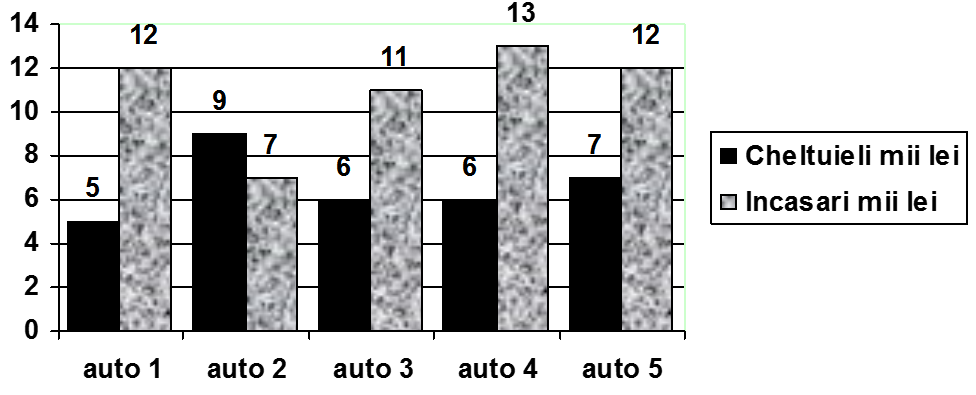
5p. 6. În diagrama alăturată sunt reprezentate veniturile si cheltuielile unei firme de taxi  cele 5 autovehicule  ale firmei pe timp de  o lună.  Care este profitul firmei pe  luna respectivă ?

    (diferenţa dintre incasări şi cheltuieli în mii  lei )

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

5p. 1. Desenaţi pe foaia de examen un paralelipiped dreptunghic numit ALGORITM

5p. 2. Enumeraţi elementele mulţimii \(A=\left\{ \ x\,\left| {} \right.unde\ x\ este\ solutie\ a\ ecuatiei\ \sqrt{{{\left( x-3 \right)}^{2}}}\cdot \left| x+5 \right|\cdot {{\left( 3x-6 \right)}^{2}}=0 \right\}\)

5p. 3.  Dacă din numărul a scad 2 , din numărul b scad 5 şi la numărul c adaug 16 obţin trei numere  a   căror medie aritmetică este egală cu 10 .

 Care este media aritmetică a  numerelor a ; b şi c ?

5p. 4.  Se consideră funcţia liniară \(f:R\to R,\ f(x)=ax+b\)

5p. a) Determinaţi valoarile lui a şi b dacă punctele A(0;–6) şi B( 8; 0) aparţin graficului funcţiei  f.

5p. b) Determinaţi aria triunghiului OMA, unde M este mijlocul segmentului AB iar O este originea   sistemului de axe.

5p. 5. Determinaţi  numerele întregi x pentru care fracţia  \(\frac{{{\left( 2x+1 \right)}^{2}}+4x+7}{2x+1}\in Z\)

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Într-un frigorifer în formă de paralelipiped dreptunghic se pun caserole (cu îngheţată) în formă de prismă patrulateră regulată cu latura bazei de 60 cm şi înălţimea de 20 cm , fară spaţii între caserole .  Se stie că pe podeaua frigoriferului  încap maxim 5 caserole   şi caserolele se aşează  în 6 straturi fără spaţii între ele.

5p. a)  Dacă într-o caserolă sunt  maxim 20 de îngheţate , aflaţi câte îngheţate  încap în frigorifer ?

5p. b) Dacă baza de superioară a frigoriferului este un capac din  plastic  ,  aflaţi suprafaţa acestei baze ?

5p. c) Care este volumul interior al frigoriferului exprimat în litri ?

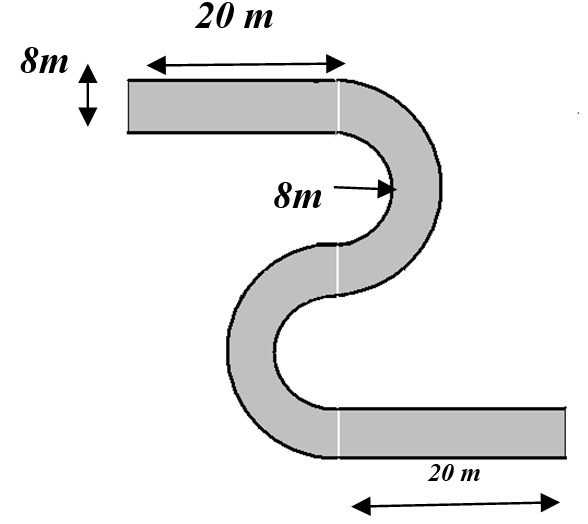
2. Figura alăturată reprezintă porţiune dintr-o şosea cu lăţimea asfaltului de 8 m  raza semicercului mic de 8 m şi  porţiunile drepte au lungimea de 20 m fiecare

(considerăm \(\pi \cong 3,14\))

5p. a)  Care este lungimea porţiunii de drum ?

5p. b)  Care este suprafaţa porţiunii de drum ?   

5p. c) Care este lungimea bordurii necesare pentru această porţiune de drum ?