Varianta 64

Prof:Conţu Valentin

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului  2⁴–2³–2² –2¹–2⁰ este egal cu……

(5p)     2. Dacă intervalul  [ – 4, a ] conţine opt numere întregi,  atunci valoarea  numărului întreg  a este  egală  cu ………

(5p)     3. Zece caiete costă 35 de lei. Patru  caiete de acelaşi fel  costa …lei

(5p)     4. Un paralelogram cu diagonalele perpendiculare şi congruente are aria de 64 cm².

  Perimetrul acestui paralelogram este …….cm.

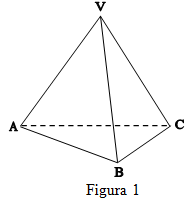
(5p)     5. În Figura 1 este reprezentat  un tetraedrul regulat VABC. Dacă  aria totală a tetraedrului este egală cu  \(36\sqrt{3}\) cm², atunci muchia tetraedrului este de …….cm.

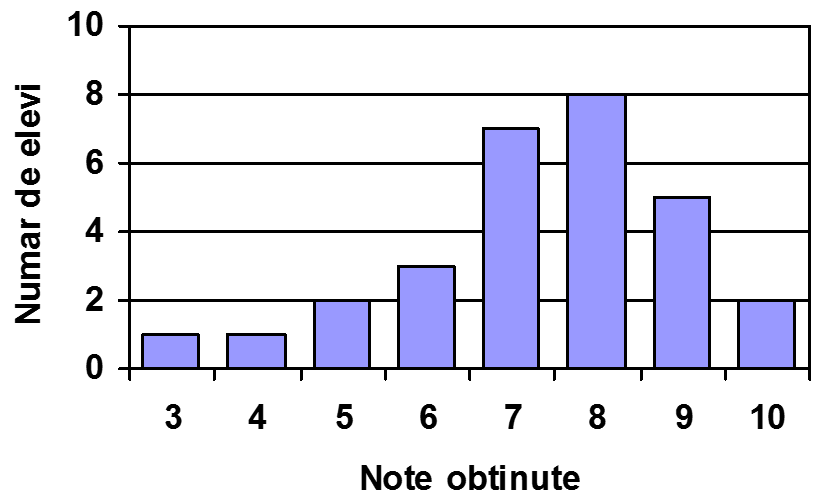
(5p)     6. Diagrama următoare prezintă situaţia notelor obţinute de elevii unei clase la teza de  matematică din semestrul I.

 Numărul elevilor din clasă este egal cu ………..

   SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi o piramidă patrulateră regulată VABCD cu baza pătratul ABCD

(5p)     2. Calculaţi  6a + 8b– 2 c , ştiind că  9a² +24ab + 16b² = 36 şi  4c = 3a + 4b, unde a, b, c∈ℝ₊

(5p)     3. Un tramvai pleacă din staţia A cu un număr de  călători. Tramvaiul trece prin staţiile  B,C,D,E,F ,G , H, I, J şi se opreşte în staţia K. Ştiind că în fiecare staţie urcă în tramvai câte 3 călători şi că în staţia B coboară un călător, apoi în următoarele staţii coboară cu un călător mai mult decât în staţia precedentă, aflaţi câţi călători au urcat în tramvai în prima staţie A, dacă în ultima staţie K mai sunt în tramvai doi călători ? 

 4. Se consideră funcţiile f : ℝ→ ℝ , cu f(x) = ax+1 şi  g : ℝ→ ℝ , cu g(x) = –x+ b  

(5p)    a) Determinaţi produsul valorile lui a şi b dacă punctul A( 2 ; 2) aparţine graficului funcţiei  f şi  B(6 ; 1) aparţine  graficului funcţiei g

(5p)    b) Dacă \(a=\frac{1}{2}\) şi \(b=7\) determinaţi aria patrulaterului determinat de graficele celor două funcţii Gf, Gg şi axele  Ox şi Oy.

(5p)     5. Dacă  a şi b sunt numere reale  şi  \({{a}^{2}}+4a+4{{b}^{2}}+4b+5=0\) , determinaţi  valoarea produsului \(a\cdot b\)

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Intr-o cofetarie se află expusă o piramidă patruleteră regulată de ciocolată cu dimensiunile bazei de 0,8 metri  şi inălţimea de 0,6   

 (5p)  a) Calculaţi apotema piramidei .

 (5p)  b) Dacă 1 decimetru cub de ciocolată are masa de 1,3 kilograme , calculaţi masa piramidei de ciocolată.

 (5p)  c)  Dacă piramida este topită si transformată în batoane de ciocolată în formă de paralelipiped dreptunghic cu dimensiunile 20 cm, 10 cm şi 2 cm , calculaţi preţul batoanelor obţinute dacă un baton de ciocolată costă 8 lei .

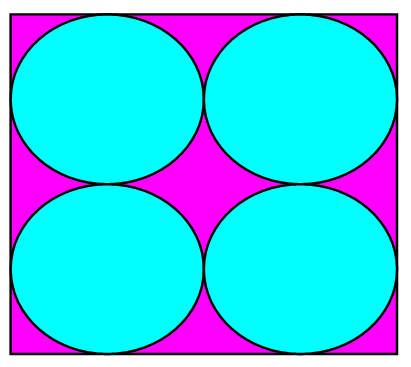
2. Figura 2 reprezintă o baterie de celule solare în formă de pătrat care conţine patru suprafeţe active în formă de disc. Latura pătratului este de 40 cm. (Discurile sunt tangente între ele şi tangente şi cu pătratul iar 3,14 < π < 3,15)

 (5p) a) Calculaţi suprafaţa activă a bateriei de celule

(5p)  b) Dacă un panou solar are formă dreptunghiulară ,  şi este acoperit complet de baterii solare iar dimensiunile  sale sunt de 1,2 m  şi 1,6 m, calculaţi suprafaţa activă a panoului.  

 (5p) c) Dacă centrele suprafeţelor active sunt legate fiecare cu fiecare prin conductori metalici , arătaţi că lungimea totală minimă a conductorilor necesari pentru o celulă solară este mai mică  decât 1,4 m.