Varianta 66

Prof: Dima Paraschiva.

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. . Rezultatul calculului \(\left( \frac{1}{2}+\frac{1}{2}\cdot 3 \right)\cdot \frac{1}{2}\) este egal cu:.................

(5p)     2. Media geometrică a numerelor \(3+\sqrt{2}\) și \(3-\sqrt{2}\)este....................

(5p)     3.Aria unui romb cu diagonalele de 15cm, respectiv 8cm este egală cu ...…cm²

(5p)     4. Numărul total de muchii la un tetraedru este egal cu:............

 (5p)     5) Se considerǎ cubul ABCDA’B’C’D’ cu aria totala de 24 cm\(^{2}\) Diagonala cubului este egala cu..........cm

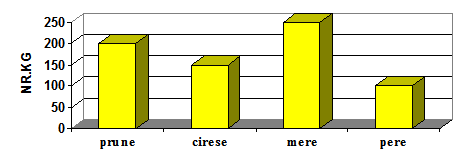
(5p)     6. Diagrama din figura 1 reprezintă cantitățile de fructe culese de un pomicultor în        anul 2011. Cantitatea  totală de fructe culese de pomicultor  este egală cu ……kg.

  SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenați pe foaia de examen o piramidă triunghiulară regulată VABC.

(5p)     2. Aratati ca numarul \({{(\frac{\sqrt{3}-1}{\sqrt{2}}-\frac{\sqrt{2}}{\sqrt{3}+1})}^{15}}\)     este intreg.

 (5p)     3. După ce a parcurs o treime din drum un călător constată că mai are de parcurs 5 km până la jumătatea drumului. Care este lungimea drumului?

4. Se consideră funcția , f(x)=2x-5.

(5p)    a) Reprezentați grafic funcția f. 

(5p)    b) Determinați coordonatele punctului de pe reprezentarea grafică a cărui ordonată este egală cu triplul abscisei.

 (5p)     5 Rezolvaţi în mulţimea numerelor naturale inecuaţia: \(\frac{3}{2}<\frac{x+2}{3}<\frac{9}{4}\).

  SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Figura 2 reprezintă suprafața unui perete al unei bucătării, AF=2m, FE=3m,ED=1m și DC=2m. Proprietarii vor să acopere suprafața peretelui cu faianță.

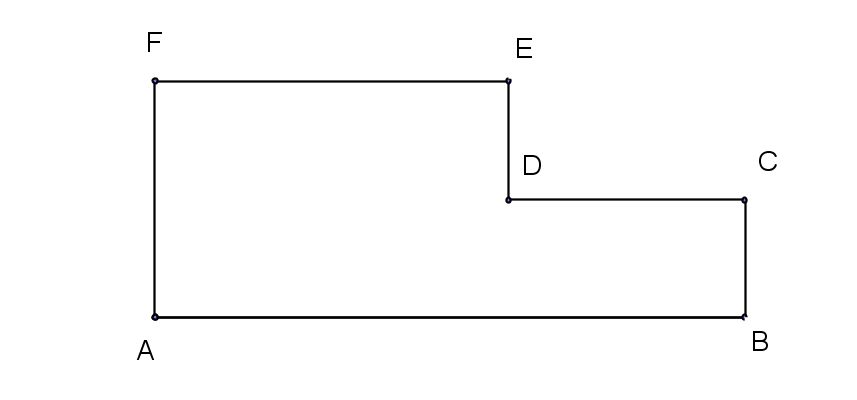
 (5p)  a) Aflați aria acestui perete.

 (5p)  b) O placă  de faianță are forma de pătrat cu latura de 10 cm. Câte plăci sunt necesare pentru acoperirea peretelui?

(5p)  c) Pentru 1m²   de faianță se plătește 125 lei, iar magazinul acordă o reducere de 5% la achiziționarea acesteia. Calculați prețul faianței necesare.

 2. Un cort are forma unei prisme triunghiulare regulate cu bazele triunghiurile ABC și DEF, AB=2 m , BE=3 m (figura 3.).

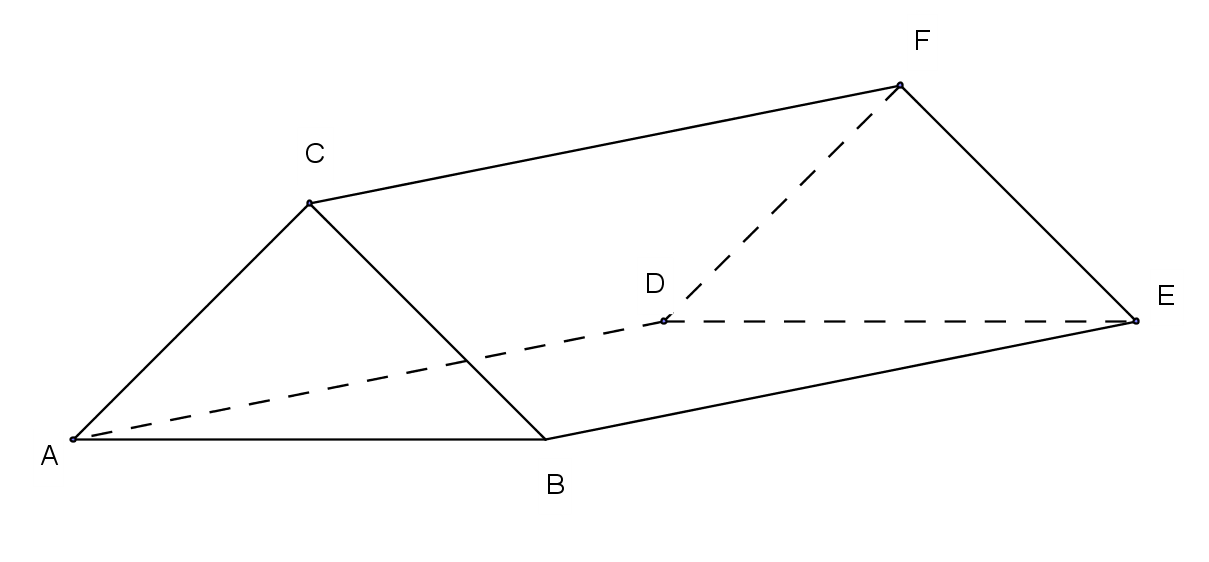
(5p)  a) Calculați volumul cortului.

(5p)  b) Două dintre fețele dreptunghiulare ale cortului sunt confecționate dintr-un material care are prețul de 75 lei/m². Cât a costat materialul dacă la cumpărarea lui s-a acordat o reducere  de 10%.

(5p)  c) Calculați, cu aproximație de o zecime prin lipsă, cea mai mare lumgime a unui băț care încape în interiorul cortului.