Varianta 75

Prof:Dorneanu Bogdan.

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului 1054 + 1054 : 2 este …………………

(5p)     2. Mulţimea \(A=\left\{ x\in \mathbb{R}/-2\le x-1<3 \right\}\) scrisă ca interval este […,…)

(5p)     3. Dacă un caiet şi trei creioane costă 12 lei, atunci trei caiete şi nouă creioane costă…… lei

(5p)     4. Într-un triunghi dreptunghic un unghi ascuţit are măsura de 30\(^{0}\), iar ipotenuza are lungimea de 12 cm. Lungimea catetei care se opune unghiului cu măsura de 30\(^{0}\) este …….. cm

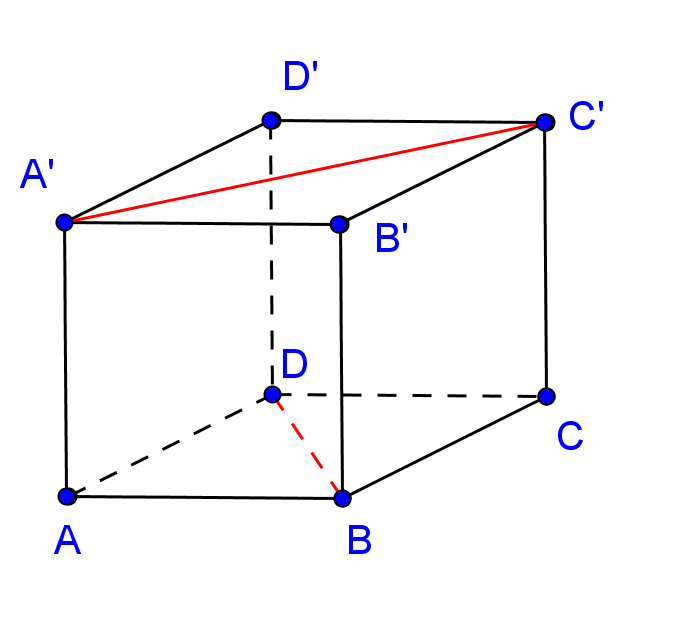
(5p)     5. În figura alăturată este reprezentat un cub \(ABCD{A}'{B}'{C}'{D}'\). Unghiului format de dreptele BD şi \({A}'{C}'\)are măsura de ……\(^{0}\).

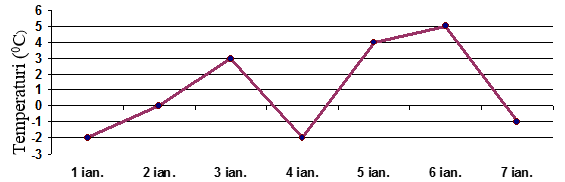
(5p)     6. Graficul alăturat prezintă evoluţia temperaturilor din prima săptămâna a lunii ianuarie a anului 2012. Temperatura media înregistrată în această perioadă este de ……\(^{0}C\).

SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi pe foia de examen o piramidă triunghiulară regulată punând în evidenţă înălţimea şi apotema piramidei.

(5p)     2. Bunicul plăteşte la piaţă suma de 12 lei cumpărând 2 kg de castraveţi şi 3 kg de morcov. Ionel, nepotul cel mai mare, plăteşte suma de 16 lei cumpărând 4kg de castraveţi şi 2 kg de morcov.  Cât costă un kg de castraveţi? Dar un kg de morcov?

(5p)     3. Să se afle trei numere naturale a căror sumă este 170, ştiind că acestea sunt direct proporţionale cu 4, 6, respectiv, 7.

 4. Se consideră expresia \(E\left( x \right)=\left( \frac{2}{x-1}-\frac{3}{x+1}+\frac{x}{{{x}^{2}}-1} \right):\frac{5}{{{x}^{2}}-2x+1}\), \(x\in \mathbb{R}\backslash \left\{ -1,\,\,1 \right\}\).

(5p)    a)Arătaţi că \(E\left( x \right)=\frac{x-1}{x+1}\), oricare ar fi \(x\in \mathbb{R}\backslash \left\{ -1,\,\,1 \right\}\).

(5p)    b)Determinaţi valorile naturale ale lui x pentru care \(E(x)\in \mathbb{Z}\).

(5p)     5. Determinaţi valorile întregi ale lui x şi y astfel încât propoziţia

\(\sqrt{{{x}^{2}}-4x+3}+\left| {{y}^{2}}+10y+21 \right|\le 0\)să fie adevărată.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

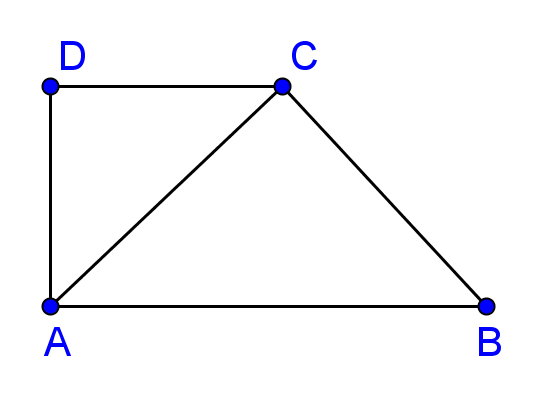
  1.Un salon are forma trapezului dreptunghic ABCD din figura alăturată. Se ştie că triunghiurile ABC şi ADC sunt isoscele şi că AB = 10m.

 (5p)  a) Determinaţi suprafaţa salonului.

 (5p)  b) Calculaţi raportul dintre aria triunghiului ADC şi a triunghiului ABC.

 (5p)  c) Pe suprafaţa ABC se pune parchet care costă 27 lei/\({{m}^{2}}\), iar că pe suprafaţa ADC se pune parchet a cărui preţ este 2 ori mai mare. Ştiind că pierderile sunt de 10% să se afle care este costul parchetării. 

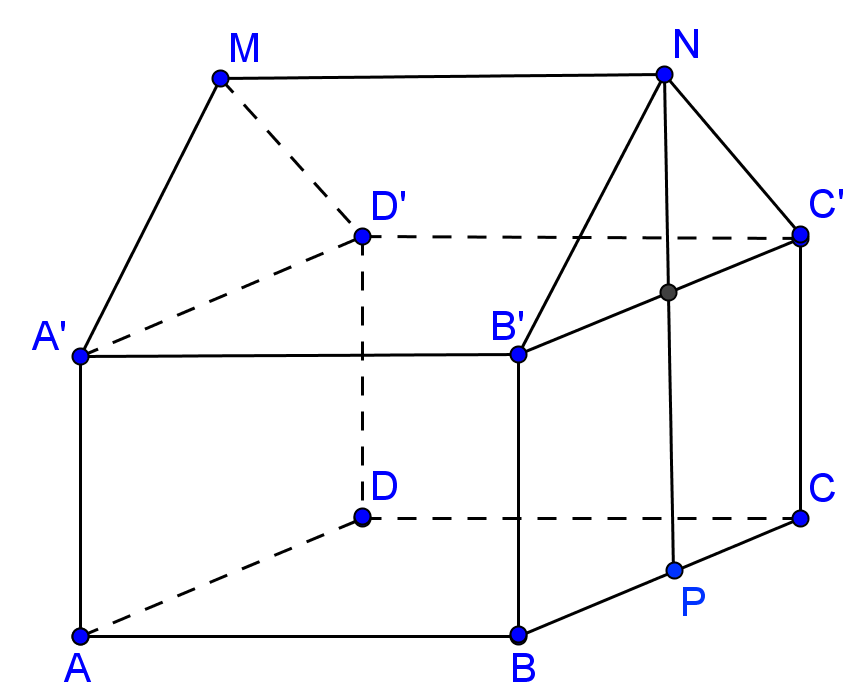
 2. O casă este prezentată schematic prin desenul din figura alăturată fiind alcătuită dintr-un paralelipiped dreptunghic ABCDA’B’C’D’şi o prismă triunghiulară regulată A’MD’B’NC’. Se ştie AB = 6m, BC = 4m, iar înălţimea casei NP este 8,4m (se consideră \(\sqrt{3}=1,7\))

(5p)  a) Determinaţi cantitatea de var necesară văruirii pereţilor casei atât pe interior cat şi pe exterior (se face abstracţie de grosimea pereţilor) ştiind că pentru 1m\(^{2}\) se foloseşte 1 kg de var.

(5p)  b) Acoperişul casei este acoperit cu ţiglă. Determinaţi cât costă ţigla, ştiind că preţul unui metru pătrat este de 52 lei

(5p)  c) Calculaţi sinusul unghiului format de dreapta D’P şi planul (ABC).