Varianta 76

Prof: Dorneanu Bogdan

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(\left( -2+3-4+5 \right):\left( 2-3+4-5 \right)\)….

(5p)     2. Soluţia naturală a ecuaţiei \({{x}^{2}}-4=0\) este x = …….

(5p)     3. Dacă din 100kg de grâu se obţin 90 kg de făină, atunci din 50 kg de grâu se obţin ……..dag de făină

(5p)     4. În rombul ABCD, \(m\left( \sphericalangle A \right)={{60}^{0}}\). Dacă BD = 6cm, atunci perimetrul rombului este egal cu ……..cm

(5p)     5. Se consideră un paralelipiped cu dimensiunile 3, 4, respectiv 5. Lungimea diagonalei paralelipipedului este ………cm.

(5p)     6. În tabelul de mai jos sunt prezentate notele obţinute de elevii clasei a V-a D la testul iniţial.

    Media clasei este …………

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi un trunchi de piramidă patrulater regulat.

(5p)     2. Se ştie că 2x – 3y = 12 şi 2y + 3z = -2. Calculaţi 4x + 9z.

(5p)     3. Determinaţi patru numere naturale, ştiind că suma lor este 150, primele trei numere sunt direct proporţionale cu 2, 3, respectiv 4, iar ultimele două numere sunt invers proporţionale cu 0,5 şi respectiv 0,(3).

 4. Se consideră funcţia \(f:\mathbb{R}\to \mathbb{R}\), \(f\left( x \right)=mx-n,\,\,\,m,\,\,n\in \mathbb{R}\).

(5p)    a) Determinaţi valorile parametrilor reali m şi n ştiind că punctele \(A\left( 2,\,\,1 \right)\) şi \(B\left( 0,\,\,-1 \right)\) aparţin reprezentării grafice a funcţiei f.

(5p)    b) Pentru m = n = 1, determinaţi aria triunghiul determinat de reprezentarea grafică a funcţiei şi axele de coordonate.

(5p)     5. Se consideră expresia \(E\left( x,\,\,y \right)=\sqrt{{{x}^{2}}-x+\frac{1}{2}}+\sqrt{{{y}^{4}}-16}\). Determinaţi valoarea minimă a expresiei \(E\left( x,\,\,y \right)\)

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Andrei, Bogdan şi Claudiu merg în excursie, aşezând corturile sub forma unui triunghi isoscel pe malul unui râu, ca în figura alăturată. Se ştie că distanţa dintre cortul lui Andrei şi cel al lui Bogdan este de 10m, iar distanţa dintre cortul lui Bogdan şi cel al lui Claudiu, care sunt aşezate pe malul râului, este de 12m.

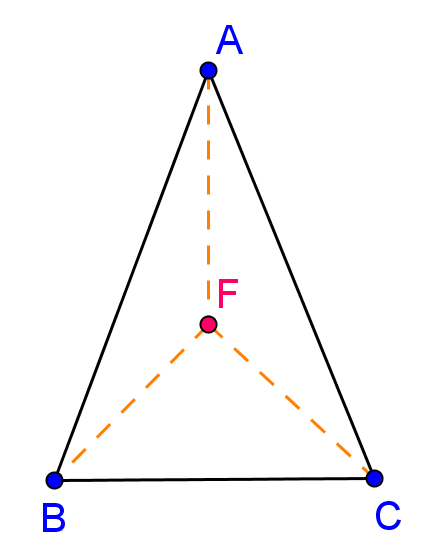
 (5p)  a) Aflaţi distanţă de la cortul lui Andrei la râu.

 (5p)  b) Să se afle unde trebuie să fie făcut focul, astfel încât acesta să se află la aceeaşi distanţă de toate corturile. Să se calculeze această distanţă.

 (5p)  c) Pentru prepararea unei supe este necesară o cantitate de 5 litri de apă. Cei trei copii dispun doar de un recipient de 250ml. Ştiind că viteza cu care se deplasează un copil de la râu pană la foc este de \(\frac{1}{4}\)m/s, calculaţi timpul necesar umplerii vasului în care se prepară supa.

 2. Un teren de joacă are forma unui trapez dreptunghic ABCD, AB\(\parallel \)CD, \(m\left( \sphericalangle A \right)={{90}^{o}}\). Pentru iluminatul terenului, în punctul B se pune un stâlp vertical cu înălţimea 5m, ancorat cu trei cabluri în punctele A, C, respectiv D. Se cunosc AB = 8\(\sqrt{3}\)m, AD = 11m şi BC = 13m.

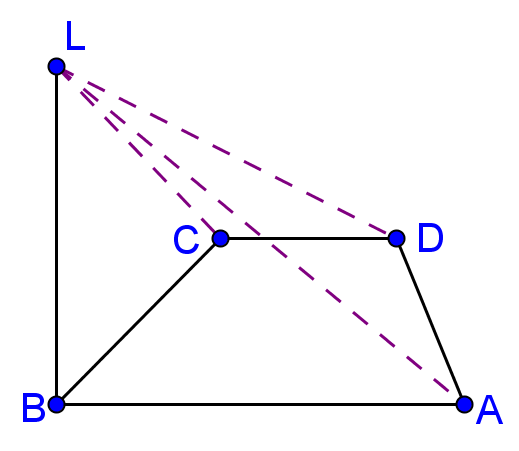
(5p)  a) Determinaţi lungimea gardului care înconjoară terenul de joacă.

(5p)  b) Calculaţi lungimea minimă a cablurilor care ancorează stâlpul.

(5p)  c) Determinaţi volumul piramidei LABCD.