Varianta 77

Prof: Dorneanu Bogdan

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(\frac{1}{2}+\frac{3}{4}:\frac{6}{4}\) este ……

(5p)     2. Cel mai mare divizor comun al numerelor 12 şi 20 este……

(5p)     3. Expresia \(4{{x}^{2}}+12xy+9{{y}^{2}}\) restrânsă ca pătrat are forma ……

(5p)     4. Diagonalele unui romb au lungimile de 6cm, respectiv 8cm. Lungimea înălţimii rombului este de …… cm

(5p)     5. În cubul ABCD, sinusul unghiului dintre dreapta AC’ şi planul (A’B’C’) este de

    ……

(5p)     6. Tabelul de mai jos reprezintă valorile obţinute de funcţia \(f:\left\{ 1;\,\,2;\,\,3;\,\,4;\,\,5 \right\}\to \mathbb{R}\).

    Atunci valoarea necunoscutei x este ……

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi o prismă patrulater regulată.

(5p)     2. Dacă \(x+\frac{1}{x}=4\), calculaţi \({{x}^{4}}+\frac{1}{{{x}^{4}}}\).

(5p)     3. Dacă adunăm la un număr necunoscut 5, rezultatul se ridică la puterea a doua, din noul rezultat se scade 4 şi rezultatul astfel obţinut se împarte la 5 se obţine 1. determinaţi numărul necunoscut.

 4. Se consideră mulţimile \(A=\left( -2;\,\,4 \right]\) şi \(B=\left[ a;\,\,5 \right)\), a\(\in \mathbb{Z}\)

(5p)    a)Determinaţi valoarea lui a ştiind că mulţimea B are exact trei elemente întregi, iar apoi calculaţi \(A\cap B\).

(5p)    b) Determinaţi valoarea lui a  ştiind că \(A\cap B\) conţine doar un număr întreg.

(5p)     5. Suma a resturilor împărţirii a 2012 numere consecutive la 2012 este de 3 ori mai mică decât suma celor 2012 numere. Care este cel mai mic număr?

  SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Figura alăturată reprezintă schema unui patinoar în care porţiunea ABCD este un dreptunghi în care AB = 10m, iar AD = 6m. Capetele patinoarului sunt două semicercuri congruente, iar punctele N şi M sunt mijloacele acestora.

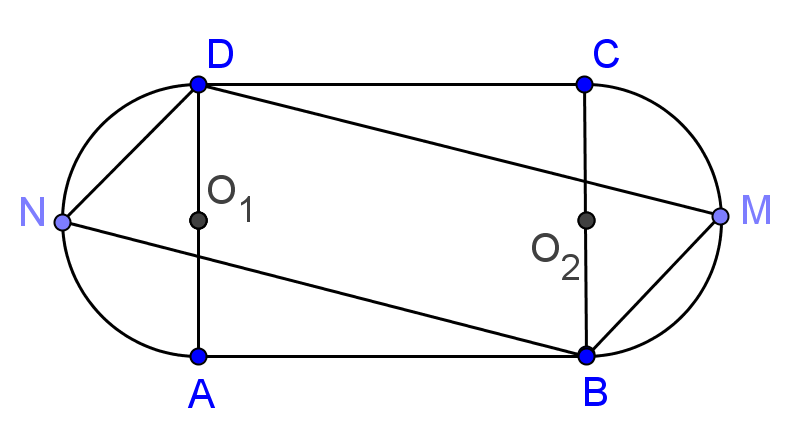
 (5p)  a) Determinaţi lungimea peretelui care înconjoară patinoarul.

 (5p)  b) Determinaţi suprafaţa patinoarului.

 (5p)  c) Un patinator parcurge traseul ABMD. Determinaţi lungimea acestuia.

2. Figura alăturată reprezintă schematic o piscină sub formă de prismă patrulater regulată cu AB = 12m şi AA’<3 Piscina este acoperită cu o umbrelă piramidală VABCD, unde VA = VB = VC = VD = 10 m.

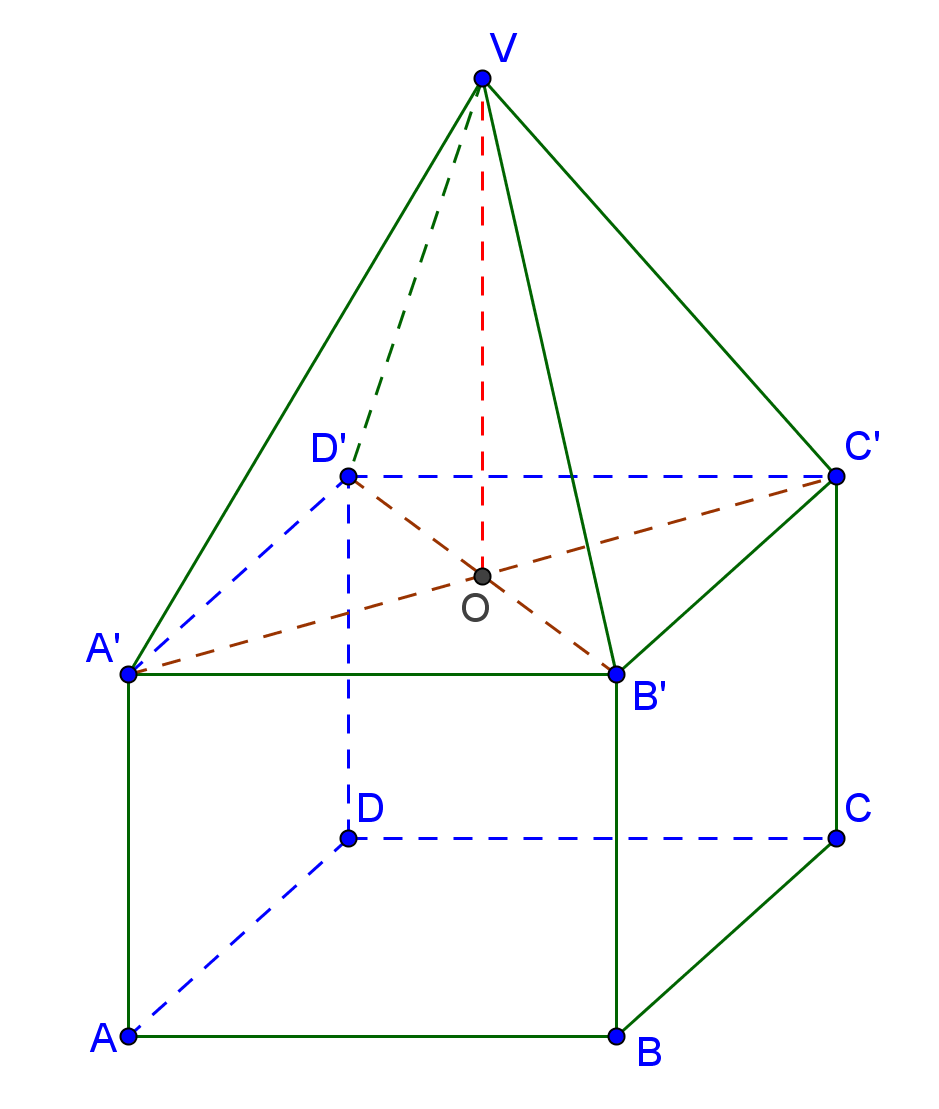
(5p)  a) Determinaţi înălţimii umbrelei.

(5p)  b) Aflaţi suprafaţa pânzei din care este confecţionată umbrela.

(5p)  c) Daca înălţimea apei din piscină este egala cu 2,5m verificaţi dacă cantitatea de apă din piscină este egală cu 360000l.