Varianta78

Prof: Gaga Loghin

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1.  18 – 72 : 4 = …...

(5p)     2.  Numărul de numere întregi din mulțimea \(\left\{ \sqrt{1},\,\sqrt{2},\,\cdots ,\,\sqrt{10} \right\}\) este : ……..

(5p)     3 5 manuale de matematică, costă 75 lei. Cât costă 3 manuale de matematică? ……..

(5p)     4. Un triunghi isoscel are măsura unui unghi 94⁰. Câte grade are fiecare dintre celelalte două unghiuri? …….

(5p)     5 Un cub cu latura de 5 cm are aria totală egală cu ……. cm²

(5p)     6.  Elevii dintr-o clasă sunt repartizați după înălțime astfel:

            Câți elevi au înălțimea mai mare și egală cu 161 cm? …….

 SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. …Desenați pe foaia de examen o priamidă patrulateră regulată cu vârful în V și bază ABCD, înălțimea VO a piramidei și apotema VM a acesteia.

(5p)     2. două numere a și b sunt invers proporționale cu numerele 0,1(6) și 0,2. Media lor aritmetică este 22. Să se determine media geometrică a numerelor a și b.

(5p)     3. Într-unul dintre laboratoarele de informatică ale școlii există cu 4 calculatoare mai puțin decât numărul de elevi ai unei grupe care face informatică. Dacă la fiecare calculator ar fi așezați câte 2 elevi, atunci 3 calculatoare ar fi libere.  Câte calculatoare sunt în laborator și câți elevi sunt într-o grupă?

 4. Graficul unei funcții \(f:\mathbb{R}\to \mathbb{R},\,\,f\left( x \right)=ax+b\), trece prin originea axelor de coordonate și prin punctul de coordonate A(-2, 4)

(5p)    a) Să se determine funcția f(x) și să se traseze graficul funcției f(x);

(5p)    b) Să se calculeze aria triunghiului format de graficul funcției f(x), originea sistemului de axe de coordonate și dreapta de ecuație y=4

(5p)     5. Știind că \(x+\frac{1}{x}=5\), să se calculeze \(E(x)=x+{{x}^{2}}+\frac{1}{x}+\frac{1}{{{x}^{2}}}\).

SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Pentru plantarea de pomi, se sapă gropi cubice ABCDA’B’C’D’, de latură 50 cm.

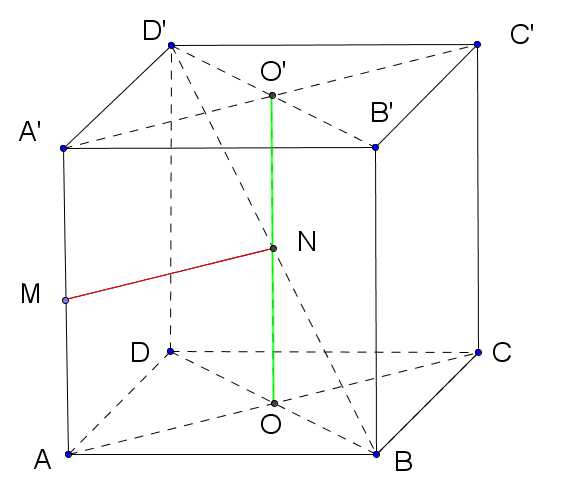
 (5p)  a) Câți metri cubi de pământ se scot pentru a finaliza o groapa?

 (5p)  b) La mijlocul muchiei AA’ fixez un punct M, iar în mijlocul gropii introduc un băț OO’ la mijlocul căruia marchez punctul N. Să se arate că \(MN\bot B{D}'\) și să se caluleze MN.

 (5p)  c) Presupunând că vopsesc pereții interiori și fundul gropii cu un amestec lichid ce conține substanțe nutritive, să se determine cât costă substanța folosită, știind că, pe 125 centimetri pătrați de perete folosesc 50 ml substanță și că un litru de substanță nutritivă costă 15 lei?

 2. Într-o grădină de forma unui triunghi echilateral ABC de latură 10 metri se consideră un punct T, arbitrar, de la care se trasează alei perpendiculare pe fiecare latură a grădinii.

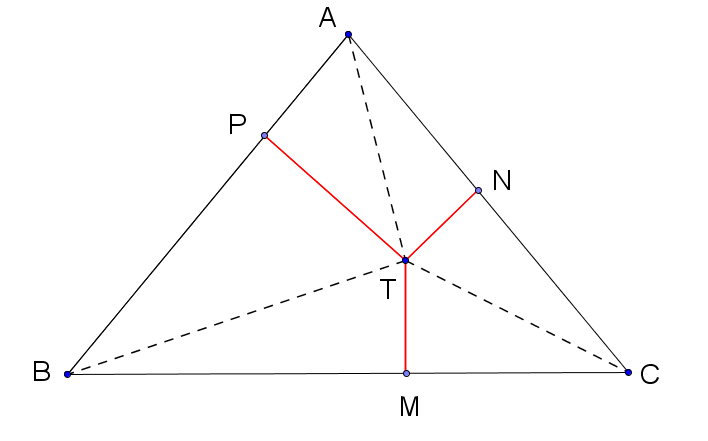
(5p)  a) Să se determine suprafața grădinii, inclusiv aleile. Se aproximază \(\sqrt{3}\,\approx 1,7\)

(5p)  b) Știind că lățimea aleilor este 30 cm, să se determine suprafața rămasă pentru a fi cultivată cu roșii, în m². Se neglijează eventualele suprapuneri.