Varianta 79

Prof: Gaga Loghin

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \({{3}^{3}}:\left( 2\cdot {{3}^{2}}+{{3}^{2}} \right)\) este :…...

(5p)     2. Media ponderată, cu ponderile 2, 3 și 6, a numerelor \(5\frac{1}{2};\,\,8;\,\,1,1\left( 6 \right)\) este: ……..

(5p)     3. Prețul unui stilou, inclusiv TVA de 24% este 25 lei. Prețul stiloului fără TVA este de …….. lei

(5p)     4. Un romb ABCD are latura de 5 cm și diagolnala mică,  BD= 6 cm. Aria rombului este de ……. cm²

(5p)     5 O prismă triunghiulară regulată dreaptă are volumul de \(45\sqrt{3}\,c{{m}^{3}}\) și aria bazei de \(9\sqrt{3}\,c{{m}^{2}}\). Înălțimea prismei este de ……. cm

(5p)     6.  20% dintre elevii unei clase formată din 30 elevi a obținut medii anuale între 5 și 6, 45% au obținut medii anuale între 6 și 8, 15% au obținut medii peste 8.

Numărul de elevi corigenți este : …..

  SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenați pe foaia de examen un triunghi oarecare ABC în care să înscriețí un cerc de centru O.

(5p)     2. Fie mulțimile \(A=\left\{ x\in \mathbb{R}\,|\,\left| 2x-1 \right|\le 5 \right\}\) și \(B=\left\{ x\in \mathbb{R}\,|\,\left| \frac{1-2x}{3} \right|>1 \right\}\). Calculați \(A\cap B\)

(5p)     3. Într-un bloc sunt 15 de apartamente cu 2 și 3 camere., în total 35 camere. Dacă 5 apartamente cu 2 camere costă cât 2 apartamente cu 3 camere și toate apartamentele din bloc costă 540 000 euro, să se determine costul unui apartament cu  3 camere.

 4. Graficul unei funcții \(f:\mathbb{R}\to \mathbb{R},\,\,f\left( x \right)=2x+a\), trece prin punctul de coordonate \(A\left( 1,\,\frac{5}{2} \right)\).

(5p)    a) Să se determine funcția f(x) și să se reprezinte grafic

(5p)    b) Pentru a= \(\frac{1}{2}\) , să se rezolve în mulțimea numerelor întregi inecuația \(\frac{3}{2}x+1\le 2f\left( x \right)+1\)

(5p)     5. Se dă expresia \(E\left( x \right)=\frac{x+2}{{{x}^{2}}+3x+2}-\frac{x-2}{{{x}^{2}}-4},\,\,x\in \mathbb{R}\backslash \left\{ -2;\,-1;\,2 \right\}\). Arătați că produsul \(\left( {{x}^{2}}+3x+2 \right)\cdot E\left( x \right)\in \mathbb{N}\), oricare ar fi \(x\in \mathbb{R}\backslash \left\{ -2;\,-1;\,2 \right\}\)

SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. În figura alăturată este prezentat un vas piramidal, cu baza un triunghi echilateral ABC și vârful V. Știind că aria laterală a vasului este \(36\sqrt{3}\,d{{m}^{2}}\) și aria sa totală este \(48\sqrt{3}\,\,d{{m}^{2}}\).

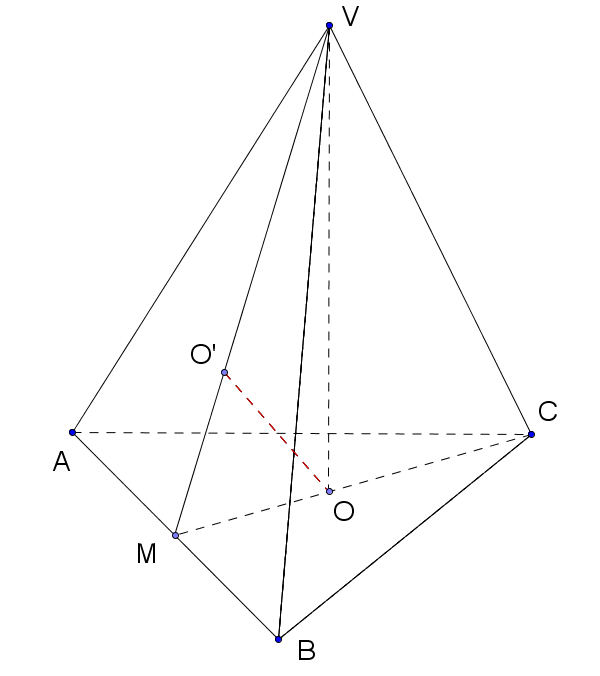
 (5p)  a) Să se determine dacă în vas încap 36 litri apă?

 (5p)  b) Cât costă vopseaua necesară vopsirii pereților laterali ai vasului, știind că pentru vopsirea a 30cm² de suprafață se folosesc 100 gr vopsea, iar un kg de vopsea costă 25 lei.

Aproximăm \(\sqrt{3}=1,7\)

 (5p)  c) Între centrele de greutate ale bazei ABC și feței VAB vrem să fixăm o tijă metalică. Calculați lungimea necesară a tijei în cm.

 2. Într-o grădină în formă de cerc cu diametrul de 60 m trebuie construite trei ronduri cu flori de formă circulară, conform figurii alăturate.

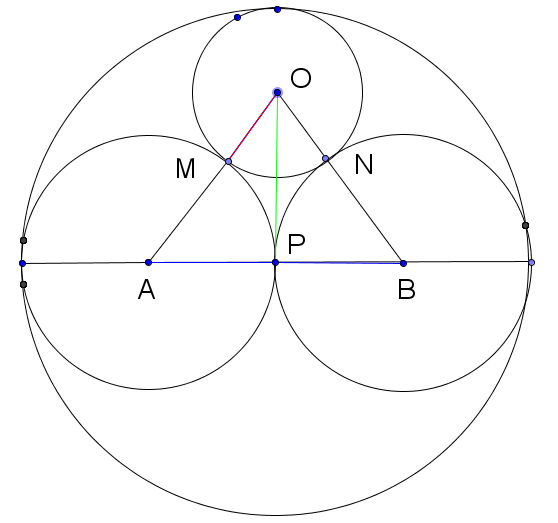
(5p)  a) Să se determine suprafața rondului mic, de centru O.

(5p)  b) Știind că în cele trei ronduri circulare se plantează flori, să se determine suprafața nefolosită , care nu se găsește în interiorul rondurilor ciculare.

(5p)  c) Știind că suprafețele care se găsesc în afara celor trei ronduri circulare se plantează cu pomi, să se determine cât se cheltuiește pentru achizițiuonarea pomilor, știind că un pom are nevoie de 12 m² de teren și că un pom costă 16,5 lei? Se aproximează \(\pi =3\). Rotunjirea se va face în sus, la întreg.