Varianta 84

Prof: Grecu Maria

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului \(18x-14x+3\cdot 5x\) este .....

(5p)     2. Se consideră funcţia \(f:\mathbb{R}\to \mathbb{R}\), \(f\left( x \right)=4x-3\). Atunci \(f\left( -3 \right)\)este egal cu .....

(5p)     3. La preţul oricărui produs se adaugă TVA de 24%. Dacă la vânzare preţul unui produs este de 42,16 lei atunci preţul produsului fără TVA este de ...... lei.

(5p)     4. Apotema unui pătrat înscris în acelaşi cerc cu un triunghi echilateral având latura de 12 cm, este egală cu ..... cm.

(5p)     5. Cubul ABCDA’B’C’D’ are muchia de lungime 15 cm. Sinusul unghiului format de diagonala BD’ cu planul (ABC) are valoarea .....

(5p)     6. Pentru evaluarea performanţelor economice reprezentanţii unei firme au realizat un grafic privind vânzările de produse realizate pe parcursul anului 2010.

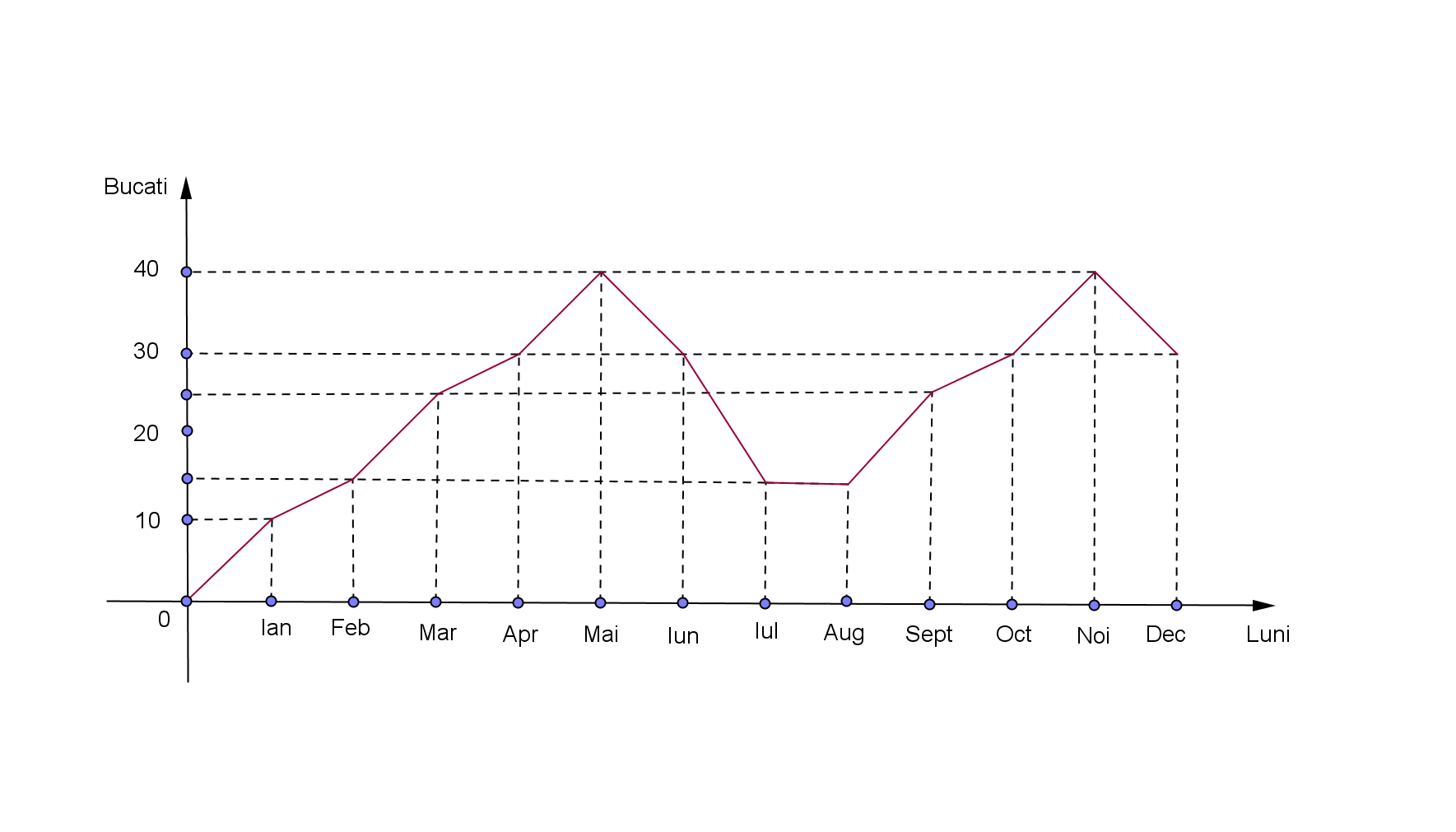
Numărul lunilor în care vânzările au fost în creştere este .....

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Să se deseneze o piramidă patrulateră regulată cu vârful în V, de bază ABCD şi cu apotema VM.

(5p)     2. Felinele de la o grădină zoologică primesc lunar o cantitate de hrană direct  proporţională cu masa lor. Un pui de leu cântăreşte 24 kg, un leu cântăreşte 100 kg iar un tigru cântăreşte 80 kg. Să se afle câte kg de hrană primeşte lunar fiecare ştiind că pentru hrana a 2 lei, 1 pui de leu şi 2 tigri se primesc 200 kg de hrană(rotunjiţi până la cel mai apropiat întreg).

(5p)     3. Reprezentaţi grafic funcţia \(f:\mathbb{R}\to \mathbb{R},f(x)=-3x+1\).

 4. Se consideră \(E\left( x \right)=\left( \frac{2}{x-1}+\frac{4}{1-{{x}^{2}}}+\frac{2}{x+1} \right):\left( 1-\frac{x}{x+2} \right)\), \(x\in \mathbb{R}\backslash \left\{ -2,-1,1 \right\}\).

(5p)    a) Să se aducă \(E\left( x \right)\)la o formă mai simplă.

(5p)    b) Să se determine \(x\in \mathbb{Z}\) astfel încât \(E\left( x \right)\in \mathbb{Z}\).

(5p)     5. Să se determine \(x,y\in \mathbb{R}\) astfel încât \(\sqrt{{{x}^{2}}-4\sqrt{3}x+12}+\sqrt{{{y}^{2}}-12\sqrt{3}+108}\le 0\) şi apoi să se calculeze media lor geometrică.

     SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. La un concurs, un alpinist trebuie să escaladeze un bloc de piatră în formă de prismă patrulateră regulată, asemeni celei din imagine. Se ştie că AB=20 şi AA’=10.

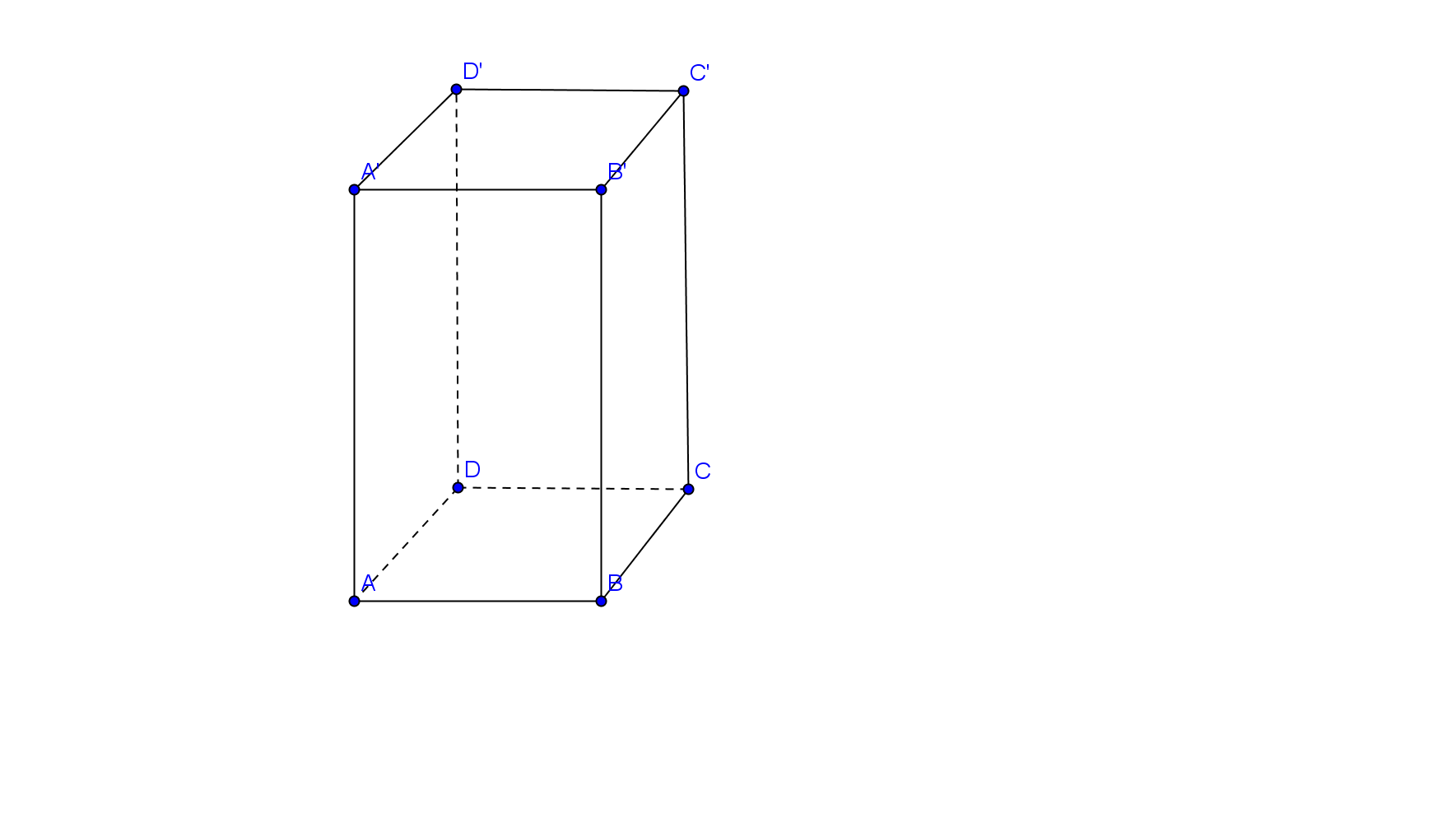
 (5p)  a) Câţi m³ de piatră conţine blocul?      

 (5p)  b) Alpinistul trebuie sa ajungă din A în A’ traversând fiecare faţă laterală a blocului. Care este lungimea minimă a traseului?

 (5p)  c) Dacă traseul alpinistului întâlneşte muchiile laterale [BB’],[CC’] în punctele P şi Q să se calculeze sinusul unghiului format de dreptele AP şi PQ.

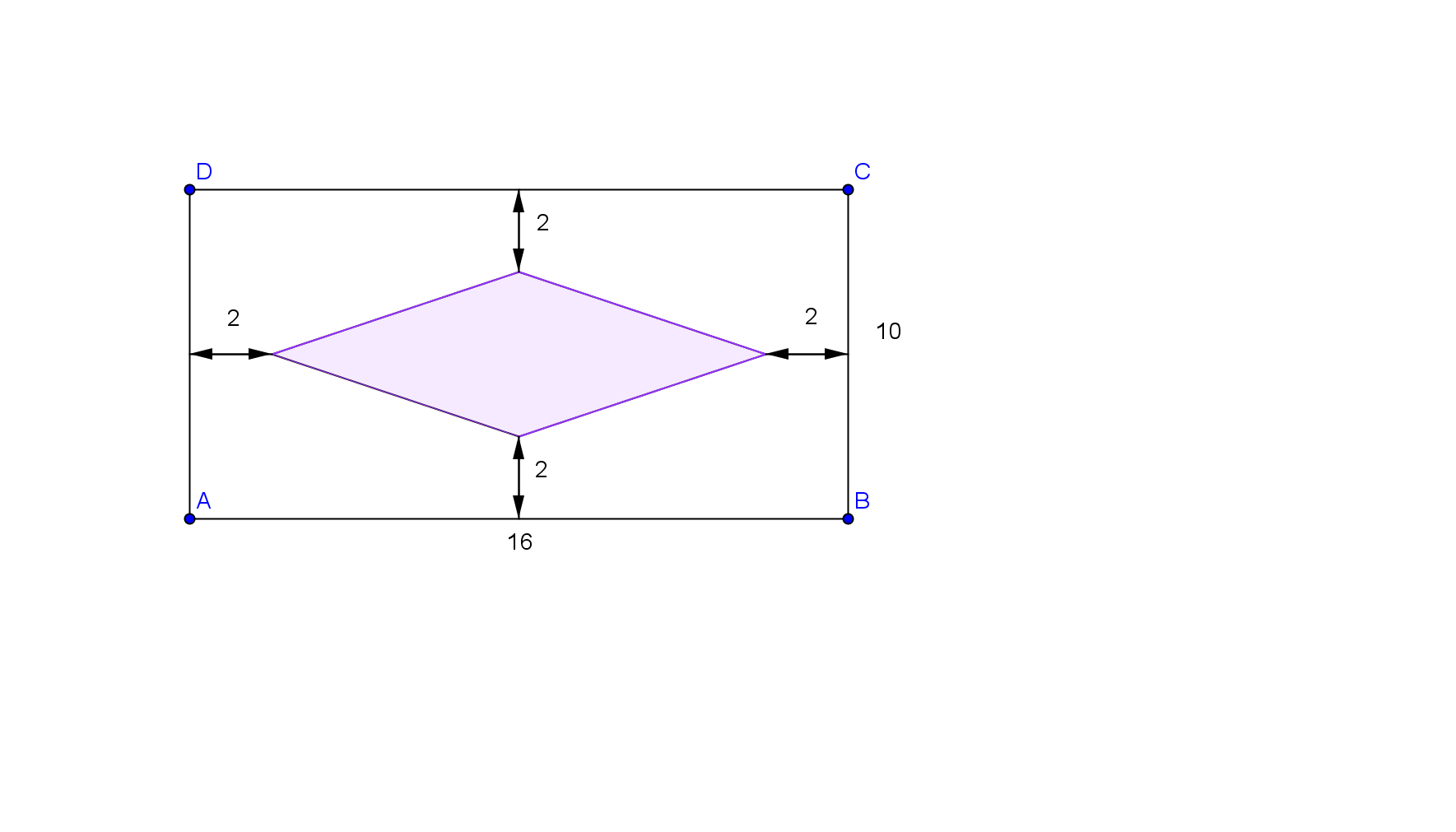
2. La o sală de dans cu ringul in formă dreptunghiulară s-a pus parchet în două culori astfel încât să alcătuiască rombul din figură(dimensiunile sunt date în metri).

(5p)  a) Câţi m² de parchet alb şi câţi m² de parchet colorat s-au folosit?

(5p)  b) Cât la sută din suprafaţa ringului reprezintă suprafaţa colorata?

(5p)  c) Cu cât ar trebui să fie egală distanţa de la un vârf al rombului până  la latura dreptunghiului astfel încât aria acestuia să fie \(\frac{1}{2}\) din aria ringului?