Varianta 85

Prof: Grecu Maria

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului \(\frac{2}{3}+\frac{1}{6}\cdot 4\)este .....

(5p)     2. C.m.m.d.c. al numerelor 72 şi 84 este ......

(5p)     3. Cardinalul mulţimii \(A=\left\{ x\in N*|(x+2)/64 \right\}\)este egal cu .....

(5p)     4. În triunghiul ABC cu \(m\left( \sphericalangle A \right)={{90}^{{}^\circ }}\)se dau AB=15 şi BC=17. Înălţimea corespunzătoare ipotenuzei are lungimea de .....

(5p)     5. Fie ABCD un trapez, AB||CD iar AD∩BC={P}. Dacă AB=20 cm, BC=12 cm, CD=15 cm şi AD=10 cm, atunci perimetrul triunghiului PAB este egal cu .....

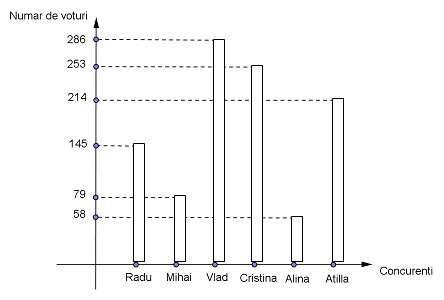
(5p)     6. La alegerile pentru funcţia de Preşedinte al Consiliului Elevilor, candidaţii au obţinut următoarele rezultate:

 Funcţia de Preşedinte a fost câştigată de .....

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi un paralelipiped dreptunghic ABCDEFGH şi trasaţi diagonala [BH].

(5p)     2. Să se determine \(x\in N\), \(x>1\), ştiind că: \({{3}^{x+2}}+2\cdot {{3}^{x+1}}-{{3}^{x-1}}=396\).

(5p)     3. Să se rezolve sistemul de ecuaţii:

\(\frac{2x-y+1}{3}=\frac{x+y}{4}\)

\({{(x-2)}^{2}}+{{y}^{2}}={{(x+1)}^{2}}+(y-3)(y+3)\)

 4. Se dau funcţiile \(f:\mathbb{R}\to \mathbb{R}\), \(f(x)=2x-4\)şi \(g:\mathbb{R}\to \mathbb{R}\), \(g(x)=-x-2\). Notăm cu A, punctul de intersecţie al graficului funcţiei f cu axa Ox, cu B şi D punctele de intersecţie ale graficului funcţiei g cu axele Oy respectiv Ox si cu C, punctul în care cele doua grafice se intersectează.

(5p)    a) Reprezentaţi grafic funcţiile în acelaşi sistem de axe ortogonale.

(5p)    b) Calculaţi aria patrulaterului determinat de graficele celor două funcţii şi axele de coordonate.

(5p)     5. Ştiind că \(x+\frac{1}{x}=4\), să se calculeze: \({{x}^{2}}+\frac{1}{{{x}^{2}}}\), \({{x}^{3}}+\frac{1}{{{x}^{3}}}\), \({{x}^{5}}+\frac{1}{{{x}^{5}}}\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. O masă de biliard are dimensiunile de 240 cm şi respectiv 120 cm.

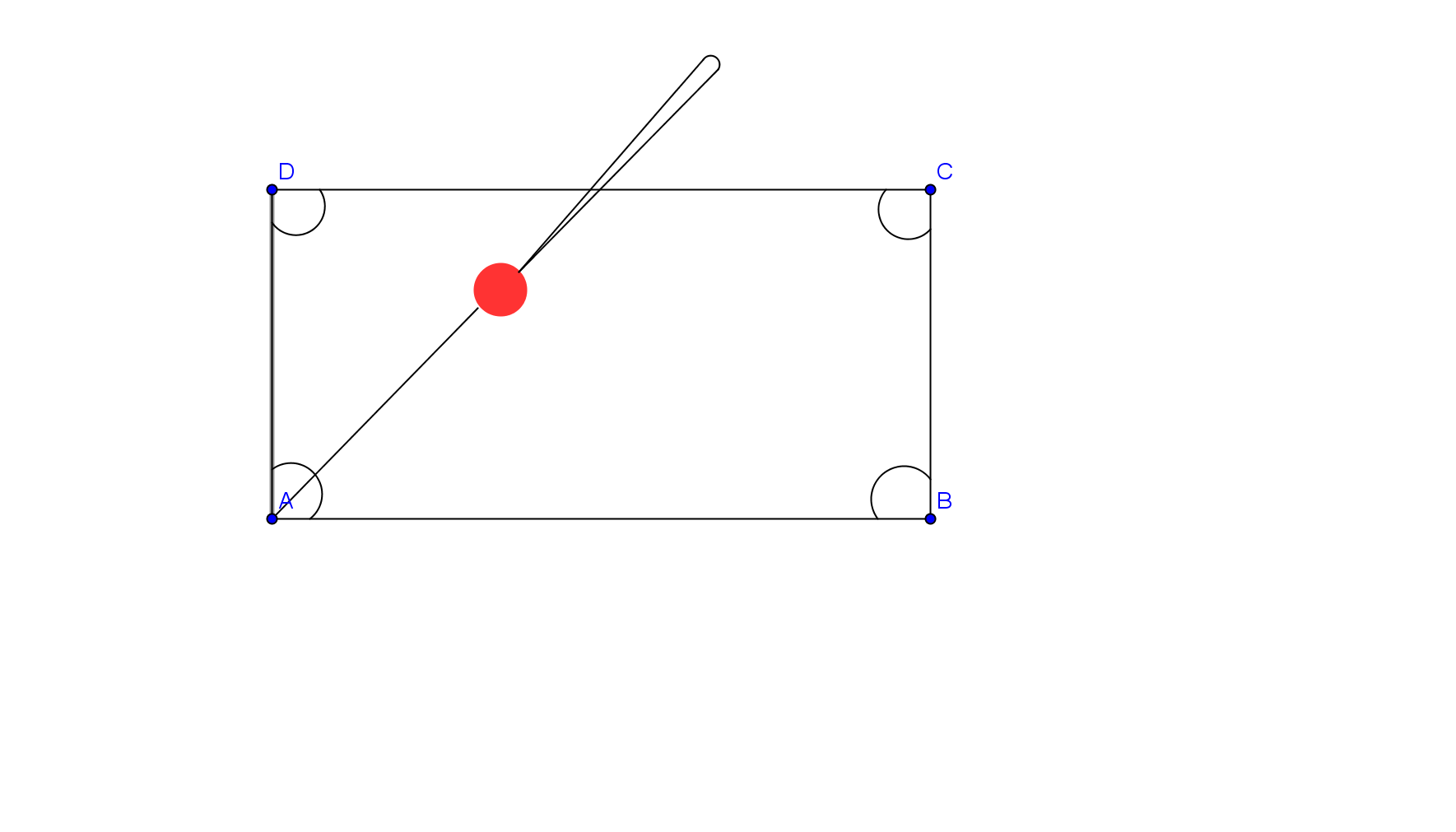
 (5p)  a) Ce suprafaţă are „terenul” de joc ( exprimaţi rezultatul in m²)?

 (5p)  b) O bilă P se află pe masă la o distanţă de 80 cm de latura AD şi 40 cm de latura DC. Ce unghi trebuie să facă tacul cu latura DC astfel încât, lovind bila, aceasta să intre în orificiul din colţul A al mesei?

 (5p)  c) Ştiind că raza bilei este 3 cm, să se afle câte rostogoliri face bila până ce cade în orificiu. (\(\pi \approx 3,14\);\(\sqrt{2}\approx 1,41\)) O rostogolire se consideră completă atunci când punctul în care bila atinge masa în momentul impactului cu tacul, efectuează o rotaţie ajungând din  nou în contact cu masa.

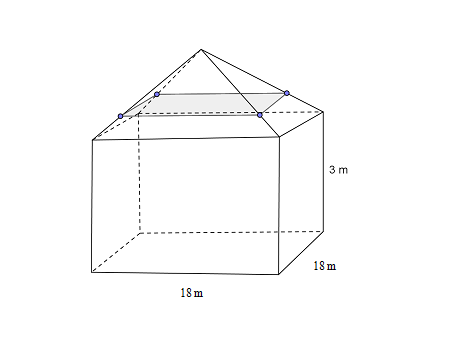
 2. Pentru desfăşurarea unui spectacol se montează un cort asemeni celui din figură. Distanţa de la vârful cortului la sol este de 5 metri.

(5p)  a) Câţi metri pătraţi de prelată au fost necesari pentru a acoperi cortul?

(5p)  b) Ştiind că pentru fiecare persoană trebuie asigurat un volum de 4 m³ de aer şi că sunt 15 persoane care asigură desfăşurarea spectacolului, să se afle numărul maxim de bilete care pot fi vândute la un spectacol.

(5p)  c) La ce distanţă de vârful cortului trebuie montată o plasă de siguranţă precum cea din desen, ştiind că aceasta are suprafaţa egală cu 225cm²?