Varianta 86

Prof:Isofache Cătălina  Anca

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului  (-2)(+2)-(-12):(+3) este…

(5p)     2. Cel mai mare număr natural de patru cifre distincte,divizibil cu 10 este…

(5p)     3. Probabilitatea ca alegând o luna a anului 2012, aceasta să aibă un număr par de zile      este...                             

(5p)     4. Un pătrat cu diagonala de 10 cm are perimetrul de ...cm.

(5p)     5. Un tetraedru regulat cu muchia de 6 cm are aria unei feţe de… cm\(^{2}\).

(5p)     6. Un stilou costă 10 lei.După o reducere de 10% preţul stiloului va fi  de...lei.

 SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi o prismă triunghiulară regulată ABCA’B’C’.

(5p)     2. Calculaţi valoarea minimă a expresiei x\(^{2}\)+4x+10 , unde x\(\in R\).

(5p)     3. Bunica Mariei a primit de ziua ei un număr de butaşi de trandafiri egal cu vârsta     împlinită.Dacă plantează câte 4 sau 6 respectiv 10 butaşi pe un rând  îi răman de fiecare dată câte 3 butaşi de trandafiri neplantaţi.Ce vârstă are bunica Mariei ?

4. Se consideră funcţia \(f:R\to R\), f(x)=\(\sqrt{2}\)-x

(5p)    a) Reprezentaţi grafic funcţia f într-un sistem de coordonate .

(5p)    b) Calculaţi distanţa de la originea sistemului de coordonate la dreapta AB,unde A(0 ;\(\sqrt{2}\)) si B(\(\sqrt{2}\) ;0).

(5p)     5. Arătaţi că expresia E(n)=\(\frac{{{n}^{2}}+6n+9}{{{n}^{2}}-9}:\frac{n-1}{{{n}^{2}}-4n+3}\) este număr întreg pentru orice valoare a lui n\(\in Z/\{-3;1;3\}.\)

    SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

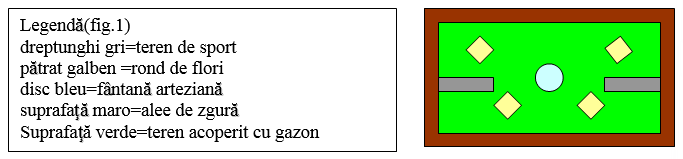
1. In figura 1 este reprezentată schiţa unui parc pe care sunt amplasate 2 terenuri de joacă de formă dreptunghiulară ,o fântană arteziană ,4 ronduri de flori şi o alee de zgură.

 Parcul este de formă dreptunghiulară cu dimensiunile de 110 m şi 90 m,aleea de zgură are lăţimea de 5 m,pătratele au fiecare latura de 5 m,cercul are raza de 5 m,iar terenurile joacă au fiecare lungimea de 30 m şi lăţimea de 20 m.

(5p)  a) Calculaţi suprafaţa aleii de zgură.

 (5p) b) Calculaţi suprafaţa acoperită de gazon.

(5p)  c) Determinaţi preţul gazonului, ştiind că acesta se vinde in lădiţe,iar o lădiţa conţine 0,5 m\(^{2}\)de gazon,preţul unei lădiţe fiind de 12 lei(în calcule consideraţi \(\pi =3,14)\).

2. La un laborator de produse alimentare se îmbuteliază esenţă de vanilie în sticluţe de 250 ml, utilizând 5 mecanisme,fiecare de forma unui cub ABCDA’B’C’D’ cu latura de 30cm,în care este introdusă o pâlnie de forma unei piramide OA’B’C’D’ ( O fiind centrul bazei ABCD). Prin orificiul A’ al pâlniei se pompează lichid cu un debit de 1,5 dm\(^{3}\)/min, iar prin orificiul O se umplu sticluţele de esenţă cu un debit de 0,5 dm\(^{3}\)/min.Pomparea lichidului prin A’ si golirea esenţei de vanilie prin orificiul O se fac simultan până când înălţimea lichidului din pâlnie ajunge la 20 cm.După care  se opreşte pomparea lichidului prin A’ şi se continuă umplerea sticluţelor prin O, până la golirea completă a pâDupă o pauză de 2 minute, pâlnia  reia automat procedeul de  funcţionare.

(5p)  a) Câte sticluţe de esenţă de vanilie  îmbuteliază un mecanism într-o oră?

(5p)  b) Dacă  mecanismele funcţionează 6 ore pe zi şi sticluţele de esenţă de vanilie se ambalează câte 30 într-o cutie,calculaţi numărul de cutii  necesare zilnic.

(5p)  c) Preţul de vânzare  al unei sticlute de esenţă de vanilie este de 1,86lei,iar TVA-ul  aplicat preţului de fabrică este de 24%.Calculaţi valoarea TVA-ului încasat din vânzarea producţiei zilnice a laboratorului.