Varianta 95

Prof:Maniţiu Blandina

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

      SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rădăcina pătrată a numărului 1225 este egală cu...

(5p)     2. Ecuaţia \(6+4x-4=10-12\) are soluţia reală \(x=\)…

(5p)     3. Dintre numerele \(a=\sqrt{19}ib=3\sqrt{2}\)este mai mare numărul....

(5p)     4. Un pătrat are aria egală cu 25 cm\(^{2}\).Diagonala pătratului este egală cu .......cm.

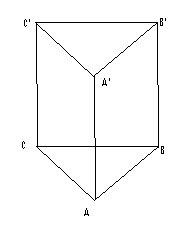
(5p)     5. Se consideră prisma dreaptă ABCA’B’C’.Măsura unghiului dreptelor  AB şi CC’este egală cu.......\(^{0}\)

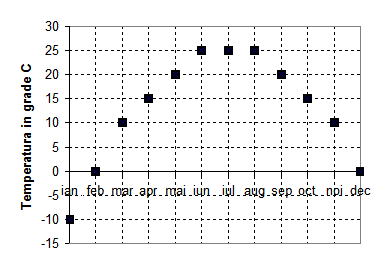
(5p)     6. În graficul de mai jos sunt redate temperaturile lunare din anul 2010 exprimate în\(^{0}C\).Atunci media temperaturilor din  lunile  august, septembrie şi octombrie este egală cu.....\(^{0}\)

    SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi un cub ABCDA’B’C’D’.

(5p)     2. Suma dintre triplul unui număr şi sfertul lui 400 este mai mică cu 15 decât

130.Aflaţi numărul respectiv.

(5p)     3. Media geometrică a două numere strict pozitive este egală cu\(\sqrt{75}\).Dacă primul număr este 15 ,aflaţi al doilea număr.

4. Se consideră expresia :\({{x}^{2}}-5x+6\),\(x\in \mathbb{R}\).

(5p)    a) Descompuneţi expresia de mai sus în factori .

(5p)    b) Simplificaţi fracţia: \(\frac{{{x}^{2}}-5x+6}{{{x}^{2}}-4},x\in \mathbb{R}\backslash \{-2,2\}\)

(5p)     5. Arătaţi că numărul \(\left| 3-2\left. \sqrt{2} \right| \right.+2\left| 1-\left. \sqrt{2} \right| \right.\in \mathbb{Z}.\)

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. O cutie are formă de paralelipiped dreptunghic cu dimensiunile de 4cm,8cm şi 2cm.

 (5p)  a)    Desenaţi paralelipipedul şi aflaţi diagonala paralelipipedului.

 (5p)  b)   Câte cubuleţe cu lungimea muchiei de 2 cm.sunt necesare pentru a umple jumătate din cutie?

 (5p)  c)    Feţele laterale ale cutiei se îmbracă cu hîrtie colorată.Aflaţi aria colii de hîrtie necesară, considerînd că înălţimea cutiei este 2 cm.

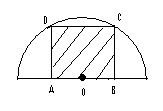
2. O foaie de tablă are formă de semidisc, raza discului din care provine semidiscul este de 3\(\sqrt{5}m.\)Un muncitor vrea să decupeze un pătrat astfel:

1. Aflaţi aria discului din care provine foaia de tablă.
2. Calculaţi latura pătratului ABCD.
3. Aflaţi raportul dintre aria pătratului şi aria semidiscului şi calculaţi cât la sută din aria semidiscului reprezintă aria pătratului.(\(\pi \simeq 3,14\)).