Varianta 96

Prof: Maniţiu Blandina

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului 117: 9-(-3)² este…    

(5p)     2. Fie mulţimile A={0,1,3,5,6} şi B={ 1,2,3,4}. AB=…..

(5p)     3. Intr-o urnă sunt 14 bile roşii şi 18 bile albe.Probabilitatea ca alegând o bilă la întâmplare,aceasta să fie albăeste egală cu.....

(5p)     4.Diametrul unui cerc este de 10cm.Lungimea cercului este…cm

(5p)     5  Aria totală a unui cub este de 96 cm². Volumul cubului este de…cm³

(5p)     6. La un concurs elevii au obţinut rezultatele conform tabelului de mai jos:

Mai mult de 6p au obţinut un număr de ........elevi

SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)    1.   Desenaţi pe foaia de teză  piramidă patrulateră regulată SUPER.

(5p)    2.  Într-un coş sunt 86 portocale şi de trei ori mai multe banane.Se consumă jumătate din numărul portocalelor şi \(\frac{2}{3}\)din numărul bananelor.Câte fructe rămân în coş?

 (5p)   3 . Mai mulţi copii vor să cumpere un obiect.Dacă fiecare dă câte 400 lei,nu ajung

2000 lei,iar dacă fiecare dă câte 500 lei, prisosesc 500 lei.Câţi copii sunt şi cât costă obiectul?

 (5p)   4. Se consideră funcţia \(f:\mathbb{R}\to \mathbb{R},f(x)=3x+4\)

(5p)    a) Stabiliţi dacă punctele A(0,4)şi B(\(-\)\(\frac{4}{3}\),0) aparţin graficului funcţiei f.

(5p)    b) Aflaţi aria triunghiului determinat de punctele de intersecţie ale graficului funcţiei f

cu axele de coordonate şi originea sistemului de coordonate xOy.

(5p)     5. Arătaţi că: (x+5)²-x-5=(x+4)(x+5)

   SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Un ornament are baza cub cu lungimea muchiei de 60 cm,peste care este suprapusă o piramidă patrulateră regulată cu lungimea muchiei laterale de 45cm,ca în figura de mai jos:

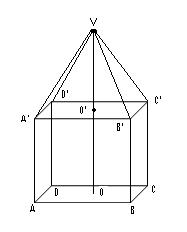
 (5p)  a) Aflaţi înălţimea întregului ornament.

 (5p)   b) Calculaţi aria hîrtiei colorate necesară pentru a acoperi toată suprafaţa exterioară a ornamentului.

 (5p)  c) Câţi litri de apă sunt necesari pentru a umple ornamentul?

2. În figura alăturată este reprezentată o placă de marmură care a fost tăiată de-a lungul segmentului MN, în două părţi pentru a realiza un pavaj.Se ştie că: AB CD,AB=120cm, CD=80cm, AD=BC=25 cm, şi MNAB,unde M (CD) şi N(AB). DM=30cm.

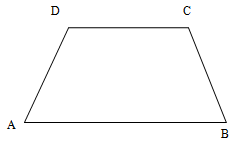
 (5p)  a) Reprezentaţi segmentul MN şi aflaţi aria suprafeţeiANMD.

 (5p)  b) Cât la sută din aria trapezului este aria suprafeţei ANMD?

 (5p)  c)  Cât costă pavarea unei suprafeţe pentru care se utilizeză 50 plăci întregi de marmură de forma ABCD, preţul unei plăci este egal cu 100 lei şi 25 de plăci de forma AMND cu preţul 40%din cel al plăciiABCD?