Varianta 97

Prof: Maniţiu Blandina

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Inversul numărului \(\frac{1}{\sqrt{2}}\)este......

(5p)     2. Ştiind că  suma a două numere este 10 ,iar produsul lor este 12 , suma pătratelor

numerelor este ……

(5p)     3 Fie\(=\{-5,\sqrt{8,}\frac{4}{5},\pi ,2+\sqrt{3},4,\sqrt{25}\}\) Se extrage un număr din mulţimea A. Probabilitatea ca numărul extras să fie număr raţional este …

.(5p)     4.  Aria unui triunghiului este triunghi echilateral este \(4\sqrt{3}\) m\(^{2}\). Atunci perimetrul....m

(5p)     5 Suma lungimilor tuturor muchiilor unui cub este de 60 cm.Atunci aria totală a cubului este egală cu.....cm\(^{2}\)

(5p)     6. În tabelul de mai jos s-au trecut cantităţile (în kg) de mere vândute într-o săptămână la un magazin. În acea săptămână s-au vândut în medie .....kg mere/zi.

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

 (5p)    1.   Desenaţi o prismă triunghiulară regulată EVALUA.

 (5p)    2.   O societate comercială are 60de angajaţi , femei şi bărbaţi. Ştiind că numărul de femei este de patru ori mai mare decât numărul de bărbaţi, aflaţi câte femei şi câţi bărbaţi lucrează la acea societate comercială.

 (5p)    3.   Determinaţi mulţimea \(\left\{ x\in \mathbb{R}/2\le \frac{x+3}{4}\le 5 \right\}\)

4. Fie funcţiile  f : R→ R, f(x) = x + 4 şi g: R→ R, g(x) = 2 x – 2.

(5p)     a)   Determinaţi coordonatele punctului de intersecţie al graficelor celor două funcţii.   

(5p)     b)   Determinaţi aria figurii cuprinsă între graficele celor două funcţii şi axa Ox.

(5p)     5.    Simplificaţi fracţia \(\frac{{{x}^{2}}+6x+9}{{{x}^{2}}-9},x\in \mathbb{R}-\left\{ -3,3 \right\}\)

         SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. În figura de mai jos este reprezentată o piramida triunghiulară regulatăVABC,cu muchia bazei de 12cm şi înălţimea VO de 10 cm.

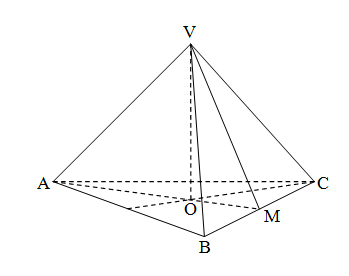
a) Aflaţi aria bazei piramidei.

b) Determinaţi apotema VM şi aria laterală.

c) Dacă la distanţa 4cm faţă de vîrful piramidei ducem un planA’B’C’paralel cu baza, aflaţi raportul dintre volumul piramidei VA’B’C’ obţinută prin sectionare şi volumul piramidei VABC .

2. În figura de mai jos este reprezentată o suprafaţă de teren ABCD, în formă de trapez dreptunghic în A , cu dimensiunile: AB = 45m, CD= 35 m, AD = 24 m. Această suprafaţă se împarte în două părţi prin linia de demarcaţie MN   paralelă cu DA. 

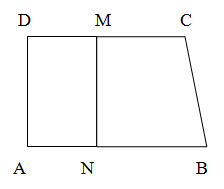
(5p)   a) Aflaţi aria trapezului ABCD.

(5p)   b) Aflaţi lungimea lui DM astfel încât suprafaţa patrulaterului NBCM să fie jumătate din suprafaţa trapezului ABCD.

(5p)   c)  Dacă DM = 20 m, aflaţi cel mai mic număr de pătrate ce pot fi înscrise în dreptunghiul ANMD.