Varianta 99

Prof:  Marcu Ştefan Florin

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Dacă 7-6+5-4+x=2 , atunci x este egal cu …

(5p)     2. Cantitatea de 60 kg de orez , a fost repartizată  în pungi de câte 6 kg . Fiecare pungă

costă 22 lei . Atunci , întrega cantitate costă  …lei .

(5p)     3  Dacă  $\frac{m}{n}=\frac{3}{4}$ , atunci  numărul m reprezintă  …% din n .

(5p)     4. Valorile numerice , a ariei şi a perimetrului unui pătrat , sunt egale.Atunci latura pătratului are lungimea de …m.

(5p)   5. Se consideră prisma dreaptă ABC${{A}^{'}}{{B}^{'}}{{C}^{'}}$.Atunci măsura unghiului dintre dreptele  A${{A}^{'}}$  şi ${{B}^{'}}{{C}^{'}}$ este de …grade.

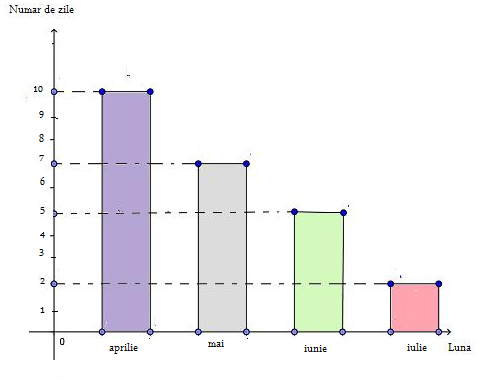
(5p)     6. Numărul de zile , în care au căzut precipitaţii într-o  ţară , de-a lungul a patru luni este prezentat conform graficului de mai jos. Atunci , media numărului de zile în care a plouat  în cele  patru luni , este de  …zile .

      SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi , pe foaia de examen,  o piramidă triunghiulară regulată , cu  vârful  V şi baza ABC .

(5p)     2. Fie A={ x$\in$R $\left| \left| 2x-1 \right| \right.<3$ } . Arătaţi că   A $\cap (Z-N)$ = $\varnothing$ .

(5p)     3. Trei caiete şi două pixuri , costă la fel ca două caiete şi trei pixuri , adică cinci lei. Aflaţi cât costă ,  împreună , un caiet şi un pix.

4. Se consideră funcţia f: R $\to$ R , f(x)=-3x+2 . 

(5p)    a) Să se afle , coordonatele punctelor de  intersecţie , dintre graficul funcţiei f , şi axele de coordonate .

(5p)    b) Aflaţi m$\in$R , astfel încât  punctul A (m,5) să aparţină graficului  funcţiei f.

(5p)     5. Arătaţi că : $\frac{\sqrt{2}+1}{\sqrt{2}-1}+\frac{\sqrt{2}-1}{\sqrt{2}+1}\in N$.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Piramida triunghiulară regulată VABC , are înălţimea de 8 m , iar raza cercului circumscris bazei este de 12 m.

 (5p)  a) Aflaţi lungimea muchiei laterale VA.

 (5p)  b) Calculaţi volumul piramidei .

 (5p)  c) Calculaţi distanţa , de la centrul bazei la o faţă laterală .

 2. Un parc de distracţii , are forma din figură . Se ştie că AB=30 m şi BC=40 m.

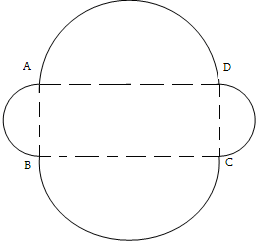
(5p)  a) Arătaţi că , lungimea gardului care împrejmuieşte parcul de distracţii , este mai mică de 221 m.

(5p)  b) Dacă notăm cu S , suprafaţa parcului , atunci , arătaţi că $\frac{S-1200}{\pi }$ este un pătrat perfect.

(5p)  c) Arătaţi că  , orice doi copii , care sunt în parc , se află la o distanţă mai mică de 105 m.