Varianta 101

Prof:  Marcu  Ştefan Florin

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Cel mai mare dintre numerele a=1+\(\frac{2}{7}\) şi b= 2- \(\frac{3}{7}\) este…

(5p)     2. La produsul dintre  numerele 125 şi 3 , adăugaţi câtul  dintre  numerele 345 şi 3 .

Rezultatul obţinut este...

(5p)     3 O ciocolată costă acum 2 lei . Dacă preţul ei creşte cu 25%  , ea va costa…lei.

(5p)     4. Într-un autobuz sunt 80 de persoane . În fiecare staţie , coboară din autobuz un număr de persoane , şi urcă , cu două persoane mai puţin . Atunci , numărul opririlor , pe care le va face autobuzul , până când în autobuz nu mai sunt persoane este de…opriri .

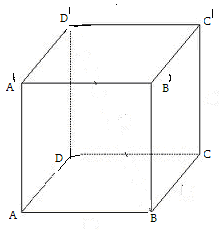
(5p)     5 Se consideră cubul din figură . Atunci măsura unghiului dintre dreptele  AD şi \(B{{B}^{'}}\)este de …grade.

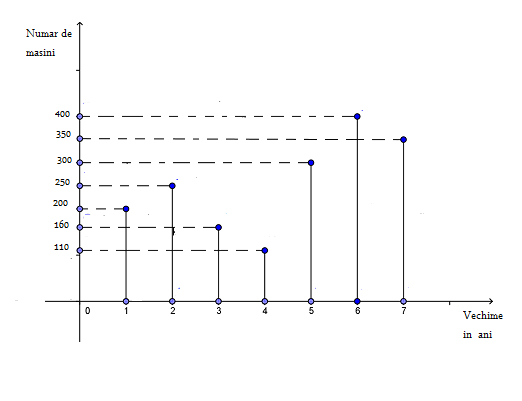
(5p)     6. Automobilele dintr-un oraş , au fost cercetate privind vechimea lor de la momentul fabricării ( în ani ) . Evidenţa lor , este conform graficului din figură . Atunci , numărul  automobilelor cu vechimea mai mică de 5 ani , este…

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi , pe foaia de examen,  o piramidă patrulateră  regulată , cu  vârful  V şi baza ABCD .

(5p)     2. Se consideră mulţimea : A={ x\(\in \)Z  \(\left| \left| 2x-1 \right| \right.<4\)} . Câte elemente are mulţimea A \(\cap \) N  ? .

(5p)     3. Un grădinar , are o grădină , în formă de pătrat , pe care plantează ceapă . El doreşte să-şi extindă suprafaţa grădinii , şi pentru aceasta , măreşte latura pătratului cu 50% .

Aflaţi  cu cât la sută , a crescut suprafaţa grădinii .

 4. Se consideră funcţia f: R \(\to \) R , f(x)=ax-2 .

(5p)    a) Aflaţi a \(\in {{R}^{*}}\) , ştiind că punctul A(1,3) aparţine graficului funcţiei f .

(5p)    b) Dacă a=5 , reprezentaţi grafic funcţia f   .

(5p)     5. Arătaţi că : \({{(\sqrt{3-2\sqrt{2}}+\sqrt{3+2\sqrt{2}})}^{2}}\in N\) .

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Se consideră un tetraedru regulat ABCD , având muchia de \(10\sqrt{3}\) m .

 (5p)  a) Aflaţi înălţimea tetraedrului. 

 (5p)  b) Calculaţi volumul tetraedrului. 

 (5p)  c) Arătaţi că , suma distanţelor , de la un punct situat în interiorul tetraedrului la feţele tetraedrului , este constantă .

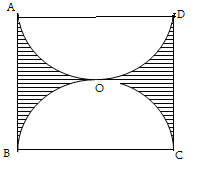
2. Grădina , în formă de pătrat din figură , are suprafaţa de un hectar , şi este împrejmuită de un gard . Suprafaţa haşurată este plantată cu pruni , iar  restul suprafeţei cu meri .

 (5p)  a) Aflaţi latura pătratului .

 (5p)  b) Arătaţi că , suprafaţa plantată cu pruni , este cuprinsă între 2125 \({{m}^{2}}\) şi 2150\({{m}^{2}}\) .

 (5p)  c) Dacă , de-a lungul segmentelor AO şi OB , s-au construit două garduri  , aflaţi lungimea gardului AOB .