Varianta 107

Prof:   Miriţă  Petruţa

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Dacă  x = 1,55 atunci [x] =... 

(5p)     2. Fie  A={x\(\in \mathbb{R}\) ç \(0\le \frac{2x+3}{3}\le 3\)}, atunci  A\(\cap \)Z...

(5p)     3.Forma simplificata a expresiei \(\frac{{{x}^{2}}-1}{{{x}^{2}}+2x+1}\)  este …

(5p)     4. Dacă  suma lungimii  muchiilor  unui  cub  este  36 cm  ,atunci   lungimea  muchiei  cubului  este...

(5p)     5.Un  romb  ABCD  are  AB=AC= 4  cm .Atunci  măsura  unghiului  ascuţit  al  rombului este...

(5p)     6. Un  litru  de  suc  de  portocale  conţine  80 % apă.Procentul   de  apă   conţinut  de  suc, dacă  Mihai  bea  o  jumătate  de  litru  este...

SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Calculaţi  : \({{\left( 2x-3y \right)}^{2}}-\left( 3x-y \right)\left( 3x+y \right)-{{\left( x-3y+1 \right)}^{2}}\).

(5p)     2.Când  s-a  născut  fiul ,mama  avea  20  de  ani  ,iar  când  s-a  născut  fiica  ,mama  avea  25  de  ani.Suma  actuală  a  vârstelor  celor  trei  persoane  este  36  de  ani.Aflaţi  vârstele  lor  actuale.

(5p)     3. Triunghiul echilateral \(ABC\) cu aria de \(15\,\,\,c{{m}^{2}}\) este baza unei piramide triunghiulare regulate cu volumul de \(75\,\,\,c{{m}^{3}}\). Aflaţi înălţimea piramidei.

4. Suma a patru numere este 690. Ştiind că al doilea număr este 80% din primul, al treilea este 75% din al doilea, iar al patrulea este 60% din al treilea, aflaţi:

(5p)    a) cât la sută din primul număr reprezintă al treilea număr?                                 

(5p)    b) cele patru numere.

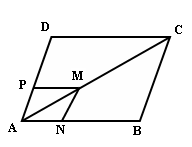
(5p)     5. În  figura   alăturată  ABCD  este  paralelogram  şi  reprezintă  o  grădină cu  lungimea  gardului AB= 40 m.Pe  lungimea aleei  AC se  construieşte   o  fântână  arteziană  în punctul M ,de  la  care  vor  porni  două  alei MN  şi MP paralele  cu  gardul  AD,respectiv AB. Dacă  \(\frac{AM}{AC}=\frac{1}{3}\) , aflaţi  lungimea  lui MP.

                                                                                           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Fie \(E(x)=\left( \frac{24{{x}^{2}}}{9{{x}^{2}}-4}+\frac{3-8x}{3x+2} \right):\frac{25x-6}{9{{x}^{2}}+12x+4}\), \(x\in \mathbb{R}-\left\{ \pm \frac{2}{3},\frac{6}{25} \right\}\)

 (5p)  a) Arătati că \(E(x)=\frac{3x+2}{3x-2}\).

 (5p)  b)  Rezolvaţi   E(x) (3x-2) -E (0) \(\le 0\),  pentru  x \(\in \mathbb{R}\) .

 (5p)  c) Pentru \(E(x)=\frac{3x+2}{3x-2}\), rezolvati ecuatia \(E(x)\cdot \frac{3x-2}{5}=\frac{2x-5}{3}\)

2. O cabană construită în satul  Sătic,comuna Podul  Dâmboviţei, are acoperişul sub  forma  unei   piramide triunghiulare regulată VABC; are latura bazei de 6 m, iar înălţimea de 12 m. Aflaţi :

(5p)  a) aria bazei  piramidei;

(5p)  b) lungimea apotemei piramidei;

(5p)  c) tangenta unghiului format de o muchie laterală cu planul bazei;