Varianta 115

Prof: Muşat Claudia

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului: \(\sqrt{3}+\sqrt{27}-\sqrt{243}\) este ....

(5p)     2. Fie mulţimea \(A=\{x\in R/\left| 2x-1 \right|\le 5\}\). Cardinalul mulţimii \(A\cap N\)este egal cu....

(5p)     3. Scara unei hărţi este 1:400000. Ştiind că distanţa reală dintre două localităţi este de   64 km, atunci distanţa din desen dintre cele două localităţi este de...cm.

(5p)     4. Un trapez isoscel ortodiagonal cu lungimea înălţimii de 9cm, are aria egală cu...cm².

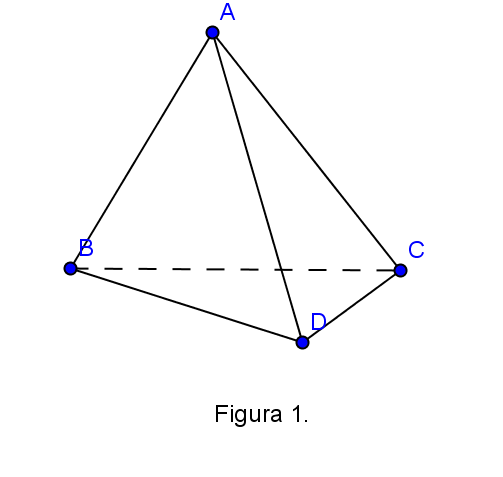
(5p)     5. În figura 1. este reprezentat un tetraedru regulat cu lungimea muchiei de 8 cm. Suma lungimilor tuturor muchiilor tetraedrului este egală cu...cm.

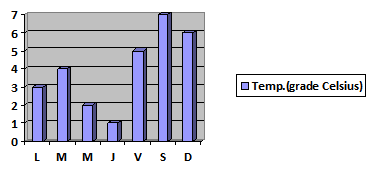
(5p)     6. Temperaturile înregistrate pe parcursul unei săptămâni sunt date de graficul următor:

Conform acestui grafic temperatura medie înregistrată în această perioadă este egală cu ...⁰C.

SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, un paralelipiped dreptunghic ABCDEFGH.

(5p)     2. Fie mulţimea\(A\times B=\{(a,b)/ab=21\}\). Calculaţi valoarea expresiei \(E(a,b)={{(a+b)}^{2}}-{{(a-b)}^{2}}\), pentru \((a,b)\in A\times B\).

 (5p)     3. Ioana şi Mihai vor să cumpere un cadou pentru aniversarea zilei de naştere a unui coleg, având împreună suma de 34 lei. Ştiind că lui Mihai îi mai lipseşte un leu, iar Ioanei îi mai rămân 3 lei şi că ei participă cu sume egale, aflaţi câţi lei a avut fiecare iniţial.

 4. Fie expresia \(E(x)=\frac{5{{x}^{3}}+10{{x}^{2}}-15x}{{{x}^{2}}+3x};x\in R-\{0,-3\}\).

(5p)    a) Simplificaţi expresia până la  forma ireductibilă.

(5p)    b) Rezolvaţi în mulţimea numerelor întregi ecuaţia: \(E(x)=2x-14\).

(5p)     5. Se consideră funcţia \(f:R\to R,f(x)=-2x+3.\)Arătaţi că \(f(3x-1)-3f(x)\in Z\) oricare ar fi x număr real.

SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Pardoseala unei săli de balet are forma trapezului din imaginea de mai jos. Ştiind că \(DE\bot AB,CF\bot AB,\)unde \(E,F\in AB\)şi \(AD=10m,DC=12m,DE=8m,FB=x\)(x este o distanţă exprimată în metri), aflaţi: 

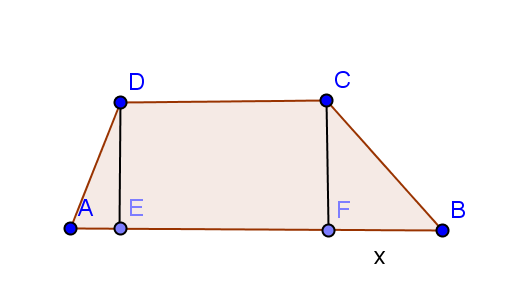
 (5p)  a)aria pardoselii sălii de balet, exprimată în funcţie de x;

 (5p)  b)pentru ce valoare a lui x, \(BC=2\sqrt{41}\)m.

 (5p)  c)costul parchetului necesar pentru parchetarea pardoselii, ştiind că  un m² de parchet costă 18,5 lei ,iar pentru achiziţionarea unor produse ce depăşesc suma de 2000 lei se acordă o reducere de 5% (se consideră x = 10m şi că nu există pierderi de material).

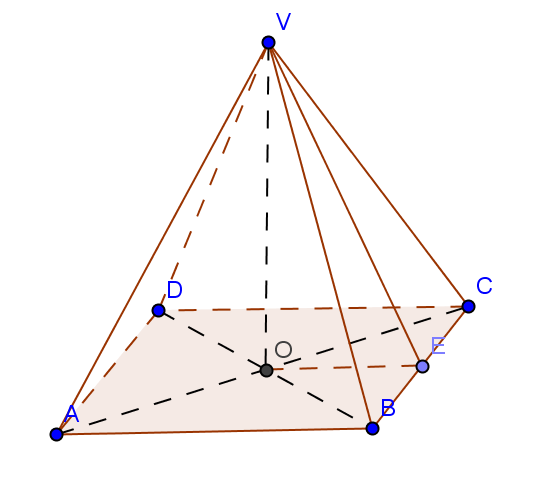
2. Acoperişul unei cabane are forma unei piramide patrulatere regulate VABCD, conform figurii alăturate, având lungimile muchiilor laterale de \(\sqrt{41}\)m şi lungimea muchiei bazei de 8m.

(5p)  a) Aflaţi înălţimea acoperişului.

(5p)  b) Aflaţi volumul acoperişului.

(5p)  c) Calculaţi costul tablei folosite pentru acest acoperiş, dacă un m² de material costă 50 lei, iar pierderile sunt de 2,5 m².