Varianta 117

Prof: Muşat Claudia.

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului:   \(2012x:x+(x-x)\cdot x\), pentru \(\forall x\in {{R}^{*}}\), este egal cu ....

(5p)     2. Opusul numărului \(-\frac{1}{5}\) este egal cu ... .

(5p)     3. Dacă \(\frac{x}{y}=2,15\) şi  \((x,y)=1\), atunci \(x+y=\)... .

(5p)     4. Diametrul cercului circumscris unui triunghi echilateral de latură \(9\sqrt{3}\)cm, are lungimea egală cu ... cm.

(5p)     5.Volumul unei prisme triunghiulare regulate este egal cu 225 cm³, iar aria bazei este de 25 cm². Lungimea muchiei laterale a prismei este egală cu...cm.                                                                                     

(5p)     6.În tabelul următor este reprezentată ponderea notelor obţinute de elevii claselor a VIII a la evaluarea naţională la matematică.

 Ponderea elevilor care au obţinut notă de promovare este egală cu ....%.

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, o prismă patrulateră regulată şi notaţi-o.

(5p)     2. Suma a două numere reale este egală cu 117. Aflaţi cele două numere ştiind că raportul lor este \(\frac{5}{4}\).

(5p)     3.Într-un coş sunt 150 mere. După ce mănâncă câteva, Andrei aşează merele rămase în coşuleţe câte 16, apoi câte 18 şi de fiecare dată îi rămân 4 mere. Aflaţi câte mere a mîncat Andrei.

4. 4. Fie expresia \(E(x,y)={{(2x-y)}^{2}}+(x-3y)(x+3y)-{{(x-2y)}^{2}}\).

(5p)    a) Aduceţi expresia la forma cea mai simplă.

(5p)    b) Calculaţi valoarea expresiei pentru x şi y care îndeplinesc condiţiile : \(\overline{2x}+\overline{5y}\)este pătrat perfect şi \(y=x+1\).

(5p)     5.Determinaţi mulţimea: \(A=\{x\in Z/\frac{x}{2}\le \frac{x-1}{5}\le \frac{2x+1}{4}\}\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. În figura de mai jos este ilustrat schematic spaţiul verde circular din mijlocul unui parc. Punctele A, B,C aparţin cercului şi reprezintă locurile unde sunt amplasaţi trei brăduţi ornamentali.Se ştie că \(m(\overset\frown{ACB})={{270}^{\circ }}\), \(m(\overset\frown{ABC})={{210}^{\circ }}\), \(AB=2x\), (\(x\)reprezintă o distanţă exprimată în metri).

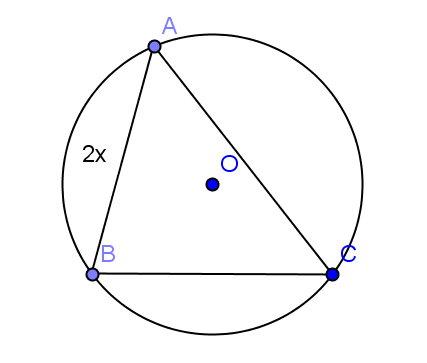
 (5p)  a) Aflaţi lungimea înălţimii din B a triunghiului ABC , exprimată în funcţie de x;

 (5p)  b) Determinaţi valoarea lui x, ştiind că \(AC=(2+2\sqrt{3})\)m.

 (5p)  c)Pentru a calcula suprafaţa rămasă, exterioară triunghiului , un muncitor trebuie să calculeze raza cercului. Determinaţi lungimea acesteia.(se consideră x= 2m)

2. În figura de mai jos sunt ilustrate schematic pardoseala ABCD şi peretele nordic CEFD al unei mansarde.(ABCD pătrat, CEFD trapez isoscel, planele determinate de cele două patrulatere fiind perpendiculare). Se ştie că: \(AB=5\) m, \(EC=4\)m şi \(m\measuredangle (EC,AB)={{60}^{\circ }}\)

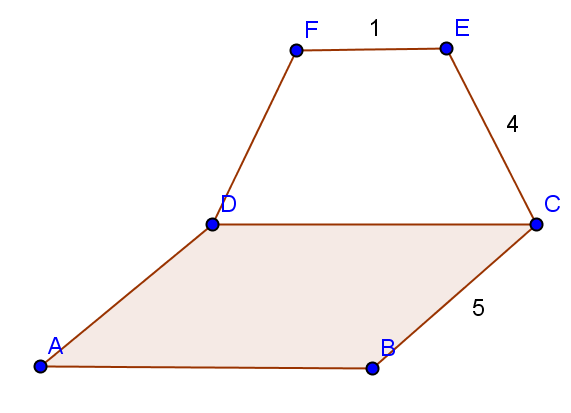
 (5p)  a) Aflaţi aria peretelui nordic.

(5p)  b) Pentru vopsirea peretelui lateral se foloseşte vopsea la preţul de 20 lei litrul, iar cu un litru se poate vopsi o suprafaţă de  2m². Câţi lei a costat vopseaua necesară? (se ia în calcul \(\sqrt{3}=1,7\)).

 (5p)  c) Calculaţi lungimea segmentului EB.