Varianta 118

Prof:  Nicolaescu Nicolae

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului 12:3·2 este egal cu….

(5p)     2. Numerele iraţionale din mulţimea \(\left\{ \sqrt{1},\sqrt{2},...,\sqrt{10} \right\}\)sunt în număr de .…

(5p)     3. Soluţia negativă a ecuaţiei \({{x}^{2}}=121\) este egală cu….

(5p)     4. Aria unui romb este egală cu 24 cm². Atunci produsul diagonalelor este egal cu….

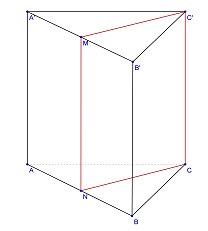
(5p)     5. În figura 1 este reprezentată o prismă triunghiulară regulată ABCA’B’C’ cu AB=10 cm, AA’=6 cm, iar M,N sunt mijloacele laturilor A’B’, respectiv AB. Aria patrulaterului NCC’M este egal cu…cm².

(5p)     6. Notele obţinute la teza de matematică de către elevii clasei a VIII-a A sunt reprezentate în tabelul de mai jos.                  

            Numărul elevilor care au obţinut cel puţin nota 7 este egal cu….

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, un triunghi echilateral ABC şi mediatoarea laturii  AB.

(5p)     2. Să se determine cel mai mare număr natural de trei cifre, cu proprietatea că împărţindu-l succesiv  la numerele 15 şi 18 obţinem de fiecare dată restul 1.

(5p)     3. Determinaţi  \(m\in R\) astfel încât punctul A(m²,m) să aparţină graficului funcţiei \(f:R\to R\), f(x)= x-6.

 4. Se consideră numerele \(a=\frac{1}{2-\sqrt{3}}+\frac{1}{2+\sqrt{3}}\) şi \(b=\frac{4}{\sqrt{2}}+{{2012}^{0}}\).

(5p)    a) Să se calculeze numerele a şi b.

(5p)    b) Să se arate că a>b.

(5p)     5. O persoană are o sumă de bani S. În prima zi cheltuieşte 50% din sumă, iar a doua zi,  \(\frac{5}{8}\) din cât a cheltuit în prima zi, constatând că i-au mai rămas 300 lei.Să se determine suma S.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. În figura 2 este reprezentată o grădină în interiorul căreia se găseşte o piscină circulară înscrisă în triunghiul dreptunghic isoscel ABC cu AB=40m.Arcul de cerc \(\overset\frown{BMC}\)este un arc din cercul cu centrul în O.

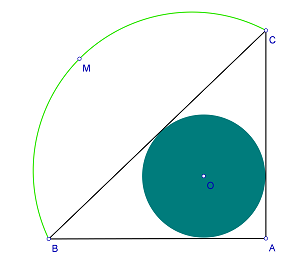
 (5p)  a) Să se calculeze suprafaţa piscinei.

 (5p)  b) Să se calculeze distanţa de la B la centrul piscinei.

 (5p)  c) Determinaţi aria grădinii.

2. Se consideră o piesă metalică în formă de prismă triunghiulară regulată ABCAA’B’C’ cu dimensiunile AB=6 cm, AA’=10 cm (figura 3)

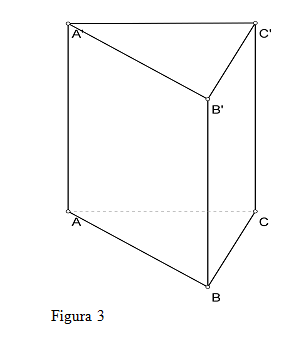
a) Să se determine cosinusul unghiului dintre planele (ABC) şi (A’BC).

b) Se secţionează piesa după planul (A’BC).Determinaţi suprafaţa corpului obţinut prin îndepărtarea piramidei A’ABC.

c) Ce procent din volumul piesei iniţiale, îl reprezintă volumul corpului îndepărtat?