Varianta 119

Prof:  Nicolaescu Nicolae

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \({{6}^{2}}-{{5}^{2}}\)este egal cu….

(5p)     2. Mulţimea \(\left\{ n\in {{N}^{*}}/\frac{1}{n}>\frac{1}{5} \right\}\) are un număr de …elemente.

(5p)     3. Cel mai mare divizor comun al numerelor 24 şi 60 este egal cu….

(5p)     4. Lungimea înălţimii corespunzătoare ipotenuzei, într-un triunghi dreptunghic isoscel cu lungimea ipotenuzei egală cu 10 cm este egală cu….

(5p)     5. Se consideră o piramidă patrulateră  regulată VABCD. Dacă volumul piramidei este 24 cm³, iar lungimea înălţimii VO este egală cu 8 cm, atunci aria pătrulaterului ABCD este egală cu…cm².                                         

(5p)     6. În figura 1 este reprezentată evoluţia profitului la o societate comercială în milioane lei, în cele patru trimestre ale anului 2011.

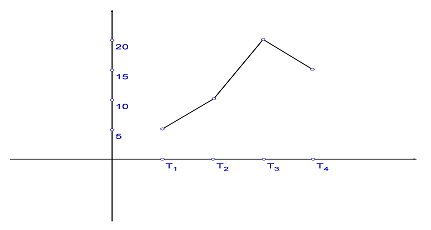Profitul mediu trimestrial al societăţii comerciale este egal cu…miliarde lei.

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, o prismă patrulateră  regulată ABCDA’B’C’D’.

(5p)     2. Să se determine cel mai mic număr natural de trei cifre \(\overline{abc}\), cu proprietatea că \(\overline{abc}+\overline{bca}+\overline{cab}=666\).

(5p)     3. Se consideră funcţia\(f:R\to R\), f(x)= 2x+3.Să se calculeze f(2)+f(2²)+…f(2¹⁰).

 4. Se consideră expresia E(x)= \(\left( \frac{1}{x+2}+\frac{1}{x-1}-\frac{2x}{{{x}^{2}}+x-2} \right):\frac{3}{{{x}^{2}}-2x+1}\), \(x\in R\backslash \left\{ 1,-2 \right\}\).

(5p)    a) Să se aducă expresia la forma cea mai simplă.

(5p)    b) Să se arate că E(\(\sqrt{3}+1\))=\(\frac{\sqrt{3}-1}{6}\).

(5p)     5. Media aritmetică a trei numere este 50.Să se afle numerele ştiind că, primul număr este de patru ori mai mare decât al doilea şi cu 6 mai puţin decât al treilea.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. În figura 2 este reprezentat un teren sub forma unui trapez isoscel ABCD cu AB=20 m, DC=100 m, EH=30 m şi două semicercuri de raze egale cu \(\frac{1}{2}\)din lungimea unei laturi neparalele.EFGH reprezintă o alee cu EF=1 m.

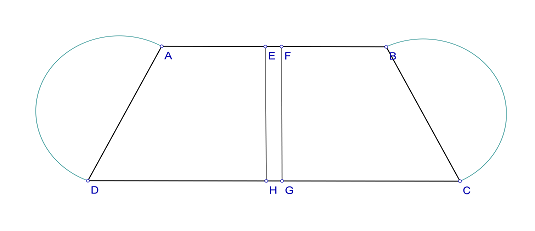
 (5p)  a) Să se calculeze suprafaţa terenului.

 (5p)  b) Să se calculeze câţi m de gard sunt necesari pentru împrejmuirea terenului (se consideră  \(\pi \simeq 3,14\)).

 (5p)  c) Dacă lungimea muchiei cubului se măreşte cu 20%, să se verifice dacă în vas s-ar putea introduce o baghetă metalică cu lungimea de 104,5 cm.

2. În figura 3 este reprezentată o cutie metalică sub forma unei prisme triunghiulare regulate , fără capac în partea superioară, cu AB=40 cm, AA’=30 cm. Punctul M este mijlocul muchiei AA’.

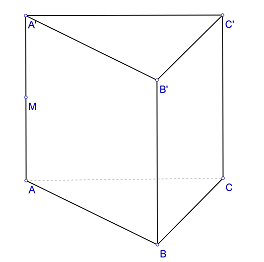
(5p)  a) Să se verifice dacă este suficientă o bucată metalică cu suprafaţa 4320 cm² pentru confecţionarea unei astfel de cutii.

(5p)  b) Să se determine cosinusul \(\measuredangle \left( \left( MBC \right),(ABC) \right)\).

(5p)  c) Se poate partiţiona cutia în patru corpuri având aceeaşi volum, prin adăugarea unor pereţi despărţitori? Justificaţi.