Varianta 120
Prof: Nicolaescu Nicolae
- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.
- Timpul efectiv de lucru: 2 ore.
SUBIECTUL I – Pe foaia de examen se trec doar rezultatele. ( 30 de puncte)
(5p) 1. Soluţia ecuaţiei 13+x=8-2 este egală cu….
(5p) 2. Media geometrică a numerelor \(\frac{1}{4}\) şi 100 este egală cu ….
(5p) 3. Suma divizorilor numărului 12 este egală cu….
(5p) 4. Aria unui triunghi isoscel ABC cu baza BC=8 cm şi \(m(\measuredangle ABC)={{30}^{0}}\) este egală cu…cm2.
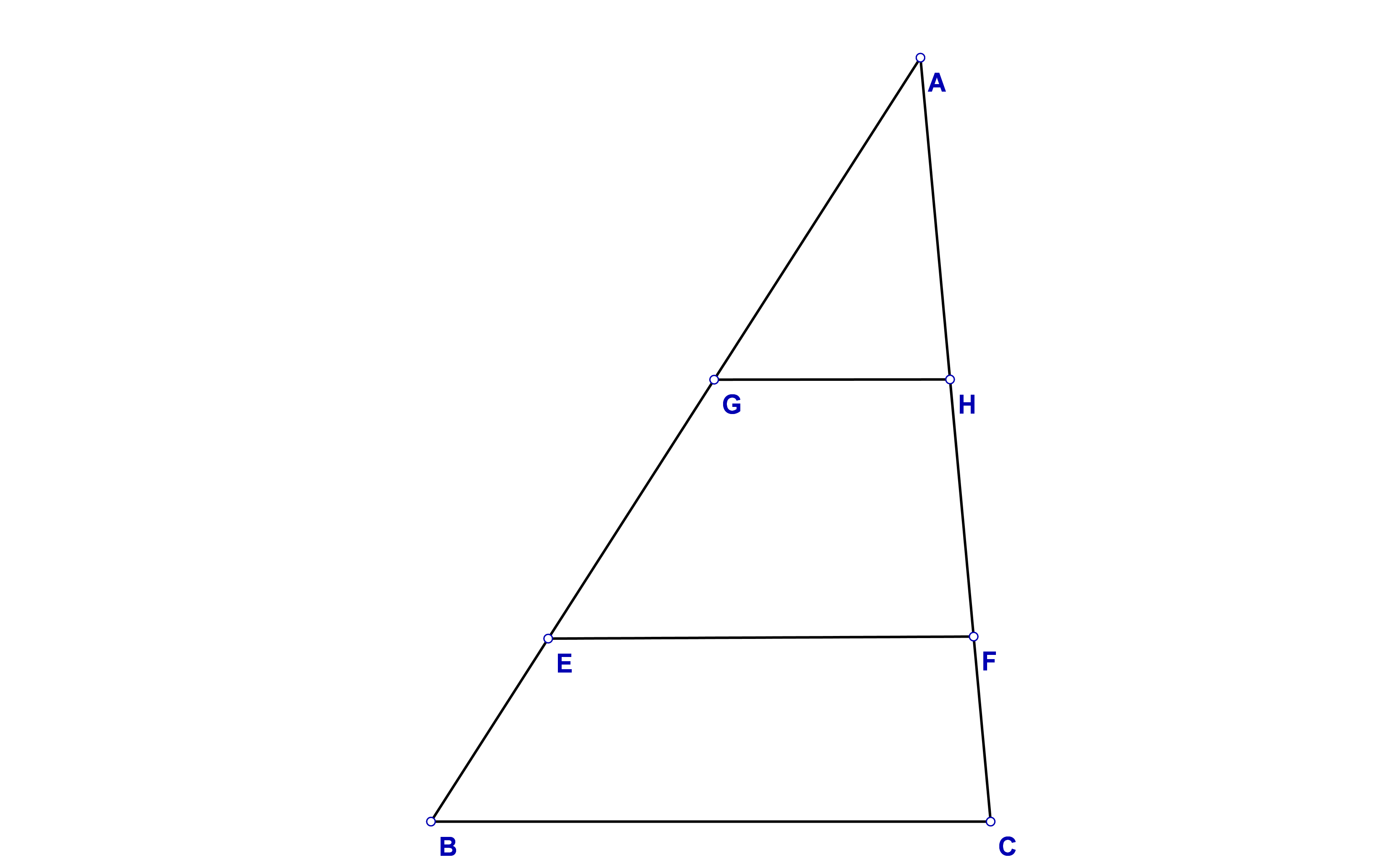
(5p) 5. În figura 1 este reprezentat triunghiul ABC cu BC=8.Se construiesc EF//BC şi GH//BC astfel încât AE=3EB şi AG=GE.Lungimea segmentului GH este egală cu…cm.
(5p) 6. În tabelul de mai jos este reprezentată evoluţia costurilor la o societate comercială în mii lei, în cele patru trimestre ale anului 2011.
|
Trimestrul I |
Trimestrul II |
Trimestrul III |
Trimestrul IV |
|
18 |
20 |
11 |
14 |
Diferenţa maximă în valoare absolută între două trimestre consecutive este egală cu…mii lei.
SUBIECTUL II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)
(5p) 1. Desenaţi, pe foaia de examen, un trunchi de piramidă triunghiulară regulată bABCA’B’C’.
(5p) 2. Se consideră ecuaţia \({{2}^{3n}}=512\), \(n\in N\). Să se determine m ştiind că \(n+m\sqrt{2}={{\left( 1+\sqrt{2} \right)}^{2}}\) .
(5p) 3. Să se determine mulţimea \(A=\left\{ x\in Z/-1\le \frac{x+3}{2}<1 \right\}\).
4. Se consideră funcţiile \(f,g:R\to R\),f(x)=-x+3, g(x)=3x-m.
(5p) a) Să se determine \(m\in R\)ştiind A(1,2) este punctul de intersecţie al graficelor celordouă funcţii.
(5p) b) Să se calculeze aria triunghiului determinat de intersecţia graficului funcţiei g cu axa Oy şi intersecţiile graficului funcţiei f cu axele de coordonate.
(5p) 5. Să se arate că \({{\left( x+3 \right)}^{3}}-x-3=(x+2)(x+3)(x+4)\), \(x\in R\).
SUBIECTUL III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)
1 În figura 2 este reprezentată o grădină unde ABDE trapez dreptunghic şi BCD triunghi echilateral cu AB=60 m, AE=40 m şi ED=x m.
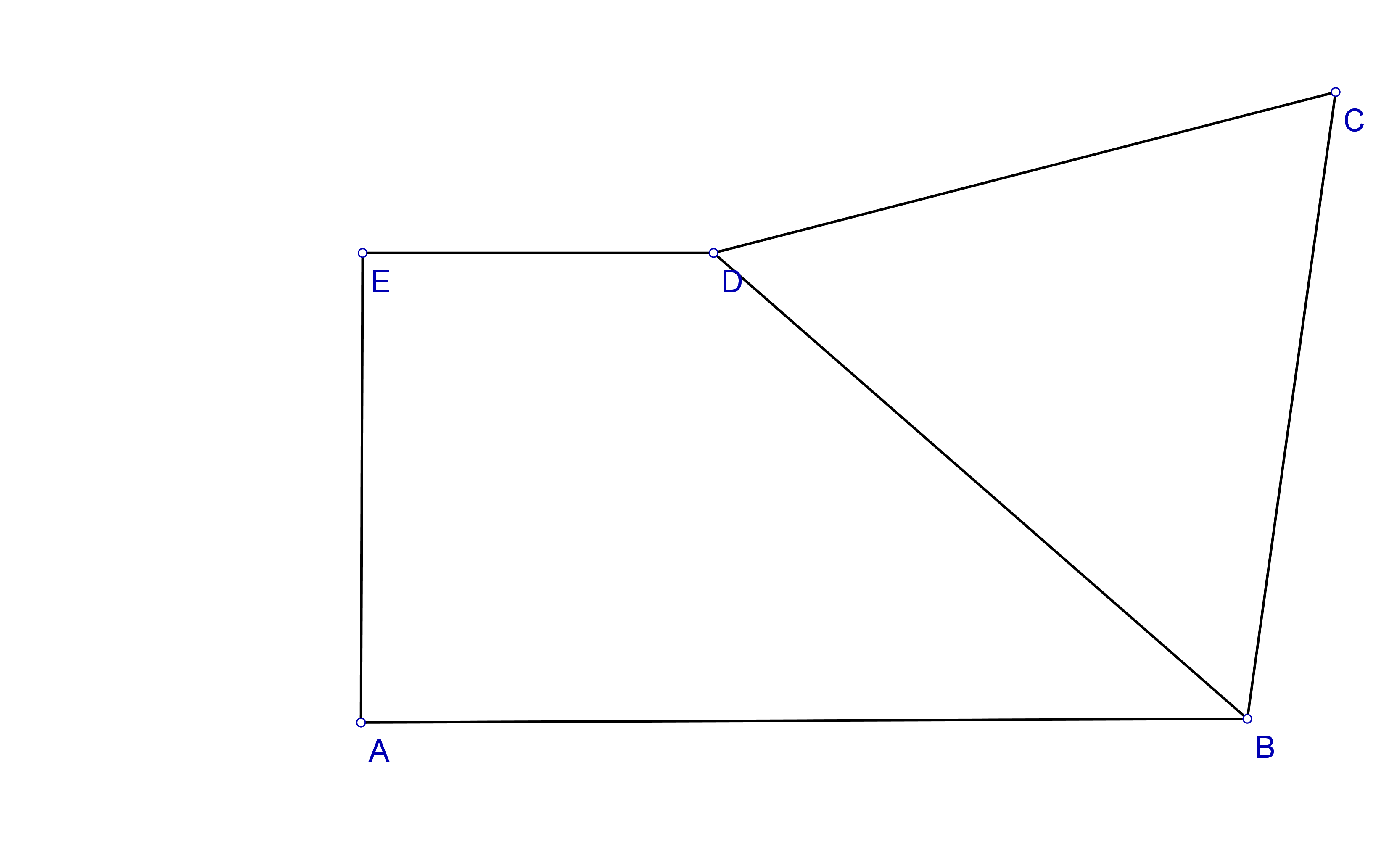
(5p) a) Să se exprime aria grădinii în funcţie de x.
(5p) b) Să se determine x ştiind că latura triunghiului echilateral este egală cu 50.
(5p) c) Dacă x=50,se poate înscrie în \(\Delta BCD\)un rond circular de flori cu suprafaţa 706,5 m2 ? (Se consideră \(\pi \simeq 3,14\))
2. Se consideră o piesă metalică de forma unui paralelipiped dreptunghic cu AB=60 cm, BC=40 cm, CC’=30 cm şi O este centrul bazei ABCD.
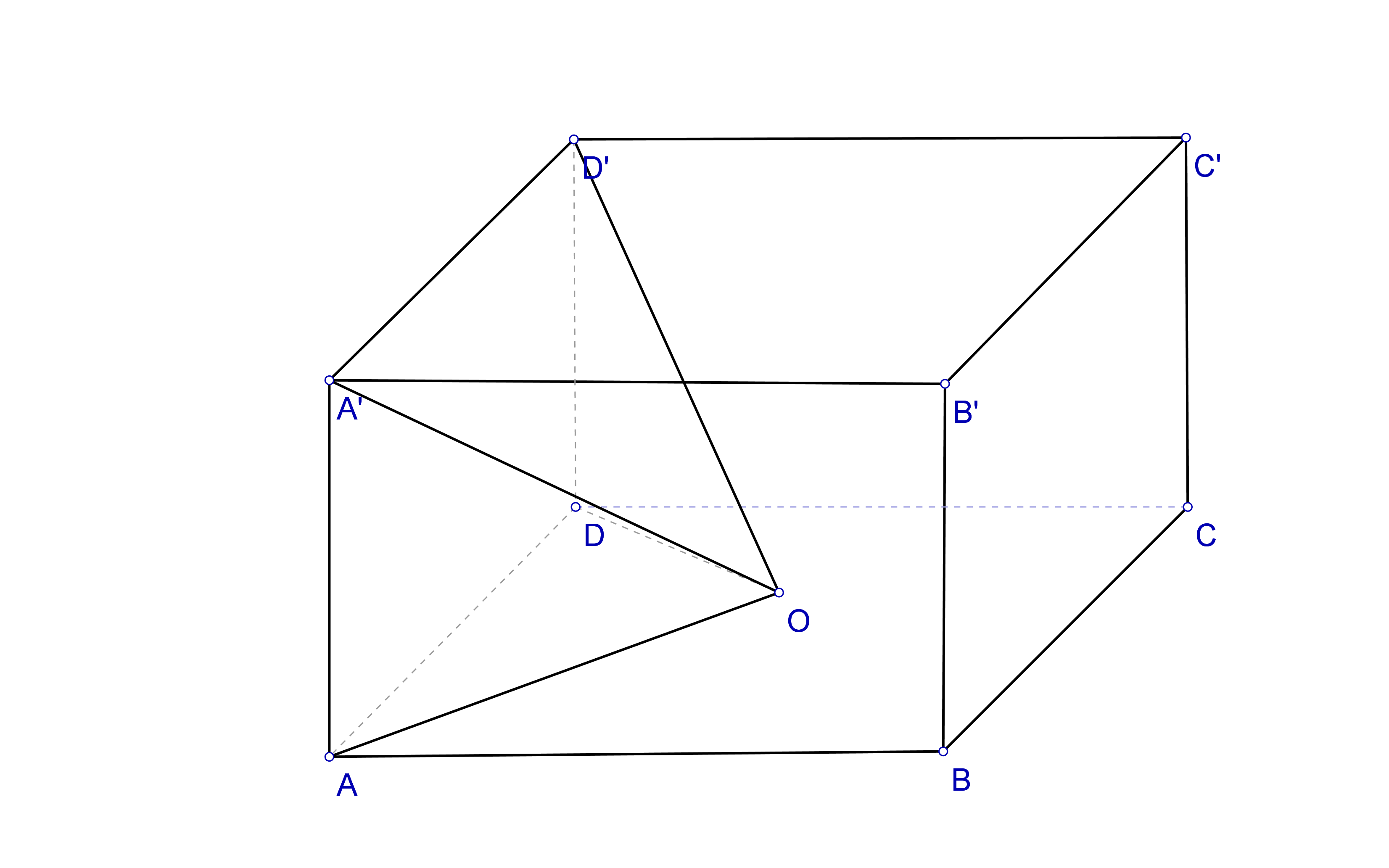
(5p) a) Să se calculeze \(\measuredangle ((OA'D'),(A'B'C'D'))\).
(5p) b) Din piesă se îndepărtează o bucată sub formă de piramidă patrulateră OAA’D’D.Să se calculeze volumul bucăţii îndepărtate.
(5p) c) Să se calculeze suprafaţa laterală a obiectului obţinut după îndepărtarea bucăţii OAA’D’D.

