Varianta 121

Prof: Nicolaescu  Nicolae

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului \(\left( -20 \right):5+4\) este egal cu….

(5p)     2. Media aritmetică a trei  numere este 24. Suma celor  trei numere este egală  cu.…

(5p)     3.Dacă adunăm un număr cu dublul său şi înmulţim rezultatul cu 4 obţinem144. Atunci numărul este…

(5p)     4.Un dreptunghi are lungimea de 6 cm şi lăţimea de două  ori mai mică. Perimetrul dreptunghiului este egal cu….cm.

(5p)     5.Fie cubul POLIEDRU cu muchia de 4 cm.Aria triunghiului ERO este egală cu…cm²

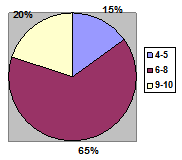
(5p)     6.În diagrama alăturată sunt reprezentate notele la teza la matematică a elevilor unei clase.Ştiind că în clasă sunt 30 elevi,numărul elevilor  care au obţinut note mai mici sau egale cu 8 este egal cu...   

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1.Desenaţi pe foaia de examen, un tetraedru regulat cu baza ABC şi vârful V.

(5p)     2.Se consideră mulţimea \(A=\left\{ x\in R/\left| 2x-1 \right|=5 \right\}.\)Enumeraţi elementele mulţimii\(A\cap N\).

(5p)     3.Suma a două numere este 105.Aflaţi numerele ştiind că  raportul lor este  \(\frac{8}{13}.\)

(5p)     4. Se consideră funcţia \(f:R\to R,\)f(x)=-(m+2)x+m.

(5p)    a) Determinaţi m\(\in R\)pentru care  punctul A(2,5) este situat pe graficul funcţiei  f.

(5p)    b) Pentru  m=1,aflaţi tangenta unghiului format de graficul funcţiei f cu axa Ox.

(5p)     5. Determinaţi  forma cea mai simplă a expresiei \(E(x)=\frac{x+1}{x-2}+\frac{x-1}{x+2}-2\), unde  \(x\in R\)\\(\left\{ \pm 2 \right\}\)

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

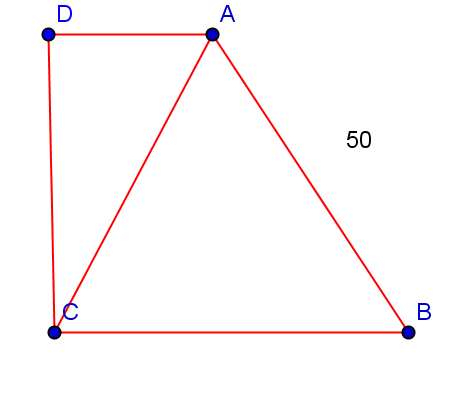
1. În figura 2 este reprezentată o grădină în formă de trapez dreptunghic cu AB =50m, iar triunghiul ABC este echilateral.

 (5p)  a) Se construieşte un gard în jurul grădinii.Aflaţi lungimea gardului.

 (5p)  b) Aflaţi aria parcelei ADC.

 (5p)  c) Determinaţi poziţia unui punct E pe latura CB astfel încât  parcelele AEB şi ECDA să  aibă aceeaşi suprafaţă.

2. Se consideră un vas în formă de trunchi de piramidă patrulateră regulată ABCDA’B’C’D’ cu  AB=5m,A’B’=2m şi OO’=3 m.

(5p)  a) Vasul este umplut cu  apă. Câţi litri de apă sunt în vas ?

(5p)  b) Se  scoate apă din vas,până la  înălţimea de 1,5 m.Cu apa scoasă se poate umple un vas cubic cu latura de  2,5 m?

(5p)  c) Care este distanţa maximă  între  două puncte ale vasului?