Varianta 123

Prof: Nicolaescu  Nicolae

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului \({{2}^{10}}:{{2}^{8}}+{{2}^{0}}\)este egal cu….

(5p)     2. Trei caiete şi cinci penare costă 21 lei.Atunci şase caiete şi zece penare de acelaşi tip costă…lei.

(5p)     3.Rezultatul calculului \({{\left( x+3 \right)}^{2}}+{{\left( x-1 \right)}^{2}}\)este egal cu…

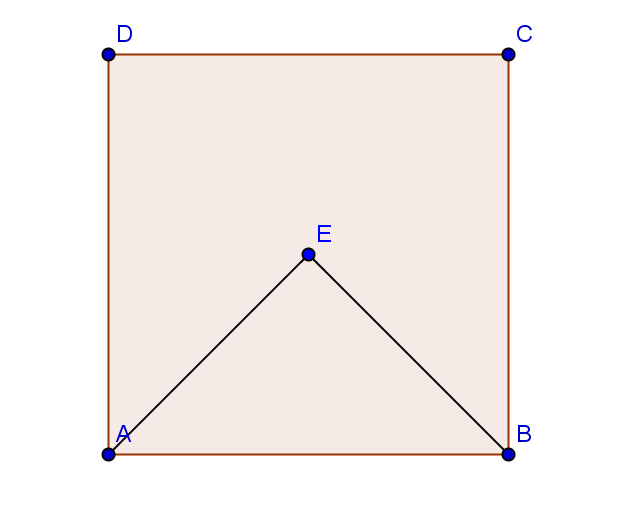
(5p)     4.În figura alăturată ABCD este un pătrat şi  punctul E este centrul său.Aria \(\Delta \)AEB reprezintă …% din aria pătratului ABCD.   

(5p)     5.Volumul unei prisme triunghiulare regulate cu latura bazei 8 cm şi înalţimea 5  cm este egală cu…cm³.

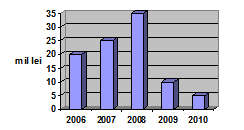
(5p)     6.În figura alăturată este reprezentată evoluţia profitului unei societăţi comerciale în perioada 2006-2010.Valoarea mediului  a profitului în această perioadă este egală cu... milioane  lei.

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1.Desenaţi,pe foaia de examen, un paralelipiped dreptunghic ABCDA’B’C’D’.

(5p)     2.Arătaţi că \(n=\sqrt{6}\cdot \left( \frac{1}{\sqrt{2}}-\frac{1}{\sqrt{3}} \right):\frac{\sqrt{12}-\sqrt{8}}{6}\) este  un număr natural.

(5p)     3.Fie funcţia \(f:R\to R\), f(x)=(m²-1)x+m.Determinaţi \(m\in R\) astfel încât punctul A(1,1) să aparţină graficului funcţiei f.

           4.Se consideră expresia \(E(x)=\left( \frac{1}{x+3}-\frac{x}{{{x}^{2}}-9}-\frac{3}{3-x} \right):\frac{x+2}{x-3}\) , \(x\in R\backslash \left\{ -3,-2,3 \right\}\).

(5p)    a) Arătaţi că \(E(x)=\frac{3}{x+3}.\)

(5p)    b) Determinaţi \(x\in Z\)astfel încât \(E(x)\in Z.\)

(5p)     5.Un biciclist parcurge un drum astfel: în  prima zi  \(\frac{1}{4}\) din drum,  a  doua zi \(\frac{2}{3}\)din rest, iar a treia zi restul de 80 km.Care este lungimea drumului parcurs de biciclist ?

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

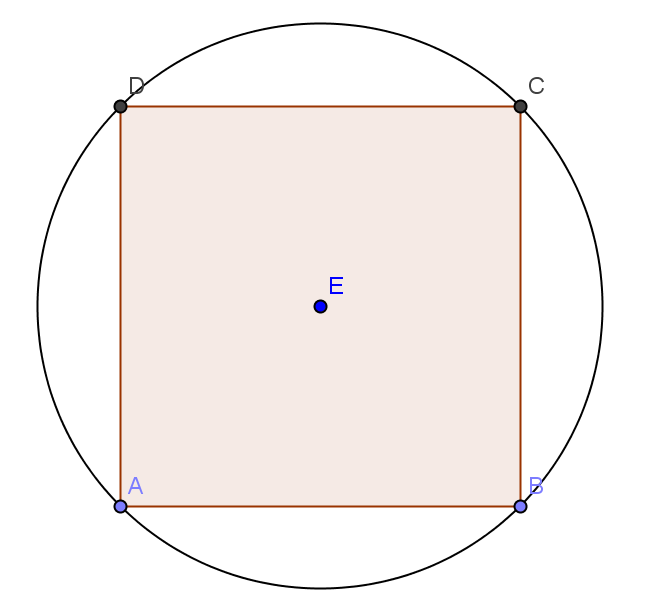
 1.Se consideră o  bucată de tablă de forma  unui disc cu raza 10 cm.

 (5p)  a) Se decupează un pătrat de arie maximă din bucata de tablă.Aflaţi aria pătratului.

 (5p)  b) Cât la sută reprezintă suprafaţa materialului înlăturat din suprafaţa bucăţii  de tablă  (se va lua \(\pi =3,14\))?

 (5p)  c) Cu  cât ar trebui mărită raza discului,pentru a  se decupa un pătrat cu aria maximă 288 cm².

2.Se consideră o piesă metalică de forma unui paralelipiped dreptunghic ABCDA’B’C’D’ cu dimensiunile 4,4,10 dm.Din această piesă se obţine o altă piesă de forma unei piramide patrulatere regulate cu baza un patrat cu latura 4 dm şi de volum maxim.

(5p)  a) Determinaţi volumul de material înlăturat pentru obţinerea noii piese.

(5p)  b) Determinaţi tangenta unghiului format de muchia laterală a piramidei cu planul bazei.

(5p)  c) Se acoperă  piesa de forma piramidei patrulatere regulate cu o foiţă de material semipreţios .Stabiliţi dacă este suficientă o foiţă cu suprafaţa de 96 dm².