Varianta 125

Prof: Oláh Csaba.

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Dacă $a,b\in {{N}^{*}}$, $a<b\le 3$ şi $\frac{a}{2}=\frac{3}{b}$, atunci $a=$...., $b=$......

(5p)     2. Restul la împărţirea numărului $n=1\cdot 2\cdot 3\cdot ...\cdot 100+62$ la $3$ este ......

(5p)     3. Rezultatul calculului $2012\cdot 101-100\cdot 2012-2011$ este .....

(5p)     4. Linia mijlocie a unui trapez este de $5cm$, iar baza mare e dublu faţă de baza mică. Lungimea bazei mari este....

(5p)     5. Suma a trei numere naturale consecutive este $24$. Al doilea număr este .....

(5p)     6. $a=2+{{2}^{2}}+{{2}^{3}}+...+{{2}^{6}}$, $b=3+{{3}^{2}}+{{3}^{3}}+{{3}^{4}}$ - mai mare dintre $a$şi $b$ este .....

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Avem cutii cu dimensiunile de $18cm$, $12cm$ şi $16cm$. Ce lungime are cel mai mic cub, care se poate construi cu ajutorul acestor cutii?

(5p)     2. Fie numerele $a=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{1024}$ şi $b=\frac{2}{4}+\frac{6}{8}+...+\frac{2046}{2048}$. Să se calculeze valoare fracţiei $\frac{a+b}{2}$.

(5p)     3. În triunghiul $ABC$ măsurile unghiurilor interioare sunt direct proporţionale cu $3,4$ respectiv $5$. Să se afle măsurile unghiurilor triunghiului.

 4. Fie mulţimile $A=\left\{ \left. x \right|{{2}^{x}}\le 32,x\in N \right\}$ şi $B=\left\{ \left. y \right|3y+1<14,y\in N \right\}$.

(5p)    a) $A,B=?$

(5p)    b) $A\Delta B=\left( A\backslash B \right)\cup \left( B\backslash A \right)=?$ (diferenţa simetrică)

(5p)     5. Desenaţi un trapez dreptunghic $ABCD$, $$\left. AB \right|\left| CD \right.$$ , $m\left( \angle A \right)=m\left( \angle D \right)={{90}^{\circ }}$.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

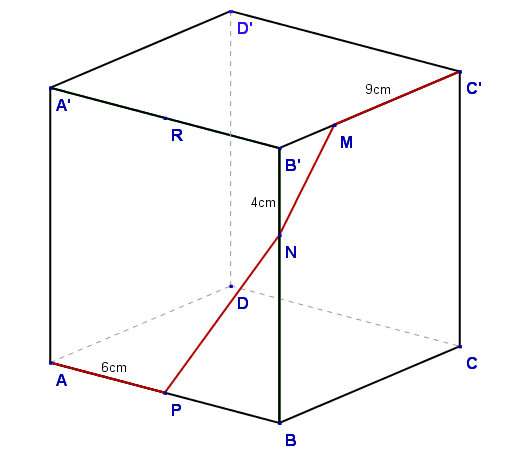
1. Fie cubul $\left[ ABCD{{A}^{'}}{{B}^{'}}{{C}^{'}}{{D}^{'}} \right]$(Fig 1.) , $AB=12cm$.

 (5p)  a) Din vârful $A$ al cubului porneşte o furnică şi vrea să ajungă în punctul ${{C}^{'}}$, parcurgând cel mai scurt drum posibil, pe suprafaţa cubului. Care va fi lungimea drumului?

 (5p)  b) Să se afle distanţa $d\left( {{C}^{'}},AB \right)$;

 (5p)  c) Fie $M\in \left( {{B}^{'}}{{C}^{'}} \right)$, $N\in \left( B{{B}^{'}} \right)$ şi $P\in \left( AB \right)$ astfel încât $M{{C}^{'}}=9cm$, $N{{B}^{'}}=4cm$ şi $AP=6cm$. Furnica se întoarce din vârful ${{C}^{'}}$în vârful $A$ pe drumul $[{{C}^{'}}MNPA]$ (marcat cu roşu pe desen). Aproximativ, cu cât este mai lung acest drum faţă de drumul din puctul a) ?

 2. Fie expresia $E\left( x \right)=\frac{{{x}^{4}}+{{x}^{2}}+1}{{{x}^{2}}+x+1}-\frac{{{x}^{2}}+x+1}{{{x}^{4}}+{{x}^{2}}+1}\cdot \left( \frac{{{x}^{4}}-{{x}^{2}}}{x\left( x+1 \right)}+1 \right)$, $x\in {{N}^{*}}$.

(5p)  a) Să se aducă $E\left( x \right)$ la forma cea mai simplă;

(5p)  b) Să se calculeze $E\left( 6 \right)$;

(5p)  c) Să se demonstreze că $E\left( x \right)\in N$ pentru fiecare $x\in {{N}^{*}}$.