Varianta 126

Prof:Oláh Csaba

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Dintre numerele \(a={{3}^{{{2}^{3}}}}\)şi \(b={{2}^{{{3}^{2}}}}\)mai mare este .....

(5p)     2. \(25%\)din dublul cincimii numărului \(250\) este......

(5p)     3. Suma a două numere naturale este \(11\) iar produsul lor \(24\). Cele două numere sunt....

(5p)     4. Dacă \(x+x+1+x+2+...+x+9=105\), atunci \(x=\)......

(5p)     5. Pentru numerotarea paginilor unei cărţi s-au folosit în total \(129\)cifre. Cartea are .....             pagini.

(5p)     6. Dacă în triunghiul \(ABC\): \(m\left( \angle A \right)={{90}^{\circ }}\), \(m\left( \angle B \right)={{30}^{\circ }}\) şi \(AC=6cm\) atunci \(BC=\)...

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Aduceţi la o formă mai simplă expresia:

\(E\left( x \right)=\frac{1}{x\left( x+1 \right)}+\frac{1}{\left( x+1 \right)\left( x+2 \right)}+...+\frac{1}{\left( x+9 \right)\left( x+10 \right)}\)

(5p)     2. O echipă de marinari, pe un vapor, are de mâncare pentru \(60\)de zile. Mai iau pe vapor \(30\)de naufragiaţi, astfel mâncarea va ajunge pentru \(50\)de zile. Câte persoane sunt pe vapor în momentul de faţă?

(5p)     3. Dacă \(E\left( x \right)=\left( \sqrt{x+1}+\sqrt{x}+\frac{1}{\sqrt{x+1}+\sqrt{x}} \right)\), \(x>0\) şi  \(a=2\cdot {{\left( \sqrt{3}+\sqrt{2}+\frac{1}{\sqrt{3}+\sqrt{2}} \right)}^{2}}\), să se calculeze \(E\left( a \right)\).

 4. Graficul functiei liniare \(f:R\to R\) trece prin punctul \(A\left( 1,1 \right)\) si este perpendicular pe prima bisectoare.

(5p)    a) Să se afle funcţia \(f\);

(5p)    b) Să se afle aria triunghiului determinat de graficul lui \(f\), axa \(Oy\) şi prima bisectoare.

(5p)     5. Să se afle aria unui triunghi cu lungimile laturilor \(13cm\),\(25cm\) şi \(12cm\)

SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Se dau mulţimile \(A=\left\{ \left. x \right|\frac{2x+5}{x-2}\in Z,x\in N \right\}\), \(B=\left\{ \left. x \right|\frac{5x-2}{3x+1}\in Z,x\in N \right\}\).

 (5p)  a) Să se determine mulţimea \(A\);

 (5p)  b) Să se determine mulţimea \(B\);

 (5p)  c) Să se calculeze probabilitatea ca alegând un element din \(A\), acesta să fie şi în \(B\).

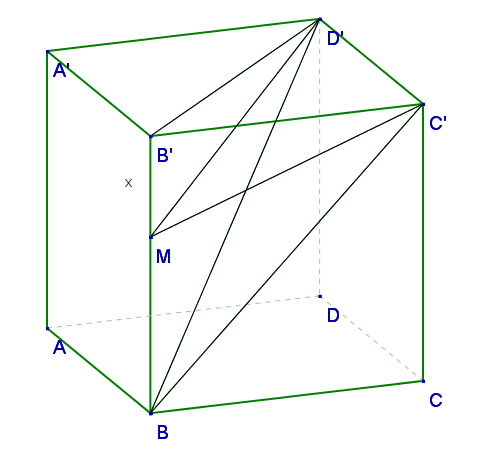
 2. Fie cubul \(\left[ ABCD{{A}^{'}}{{B}^{'}}{{C}^{'}}{{D}^{'}} \right]\)(Fig 1.) , \(M\in \left( B{{B}^{'}} \right)\) şi \({{B}^{'}}M=x\).

(5p)  a) Dacă \(x=2\sqrt{3}\) şi \(M{{C}^{'}}=2{{B}^{'}}M\), să se afle \(AB\);

(5p)  b) Dacă \(AB=6cm\), să se afle \(MD\);

(5p)  c) Dacă \(AB=6cm\), să se calculeze raportul \(\frac{{{V}_{\left[ BM{{C}^{'}}{{D}^{'}} \right]}}}{{{V}_{\left[ ABCD{{A}^{'}}{{B}^{'}}{{C}^{'}}{{D}^{'}} \right]}}}\).