Varianta 127

Prof: Oláh Csaba

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Ultima cifră a numărului \(n=1\cdot 2\cdot 3\cdot ...\cdot 99+1\) este....

(5p)     2. Rezultatul şirului de operaţii \(3654\cdot 1236-1235\cdot 3654-3653\) este.....

(5p)     3 Doi biciclişti pornesc în acelaşi timp din localităţile \(A\)şi \(B\), unul spre celălalt. Primul circulă cu viteza de \(15km/h\), al doilea cu \(20km/h\), drumul lor ţine mai mult de o oră. Distanţa dintre ei, inainte cu o oră de a se întâlni va fi ......

(5p)     4. Dacă \(3ax-12bx=36\) iar \(a-4b=6\), atunci \(x=\).....

(5p)     5. Un produs s-a scumpit cu \(20%\), iar peste o săptămână s-a ieftinit cu \(10%\). După ieftinire produsul este mai scump cu .....\(%\)faţă de preţul iniţial.

(5p)     6. Dacă \(f:R\to R\) , \(f\left( x \right)=2x+3\) atunci \(f\left( 0 \right)+f\left( 1 \right)+...+f\left( 10 \right)=\)......

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Să se demonstreze că numărul \(a=n\left( n+1 \right)\left( n+2 \right)+1\) nu este divizibil cu \(3\), \(n\in {{N}^{*}}\).

(5p)     2. Să se deseneze o piramidă patrulateră regulată.

(5p)     3. Să se demonstreze că suma primelor \(20\)de numere prime nu se împarte la \(2\).

4. Pentru o lucrare s-au prezentat trei muncitori. Primul, daca ar lucra singur, ar termina lucrarea intr-o oră, al doilea în \(3\)ore iar al treilea in \(2\)ore.

(5p)    a) În cât timp ar termina lucrarea dacă ar lucra împreună?

(5p)    b) În cât timp ar termina lucrarea împreună, dacă ar mai chema un muncitor, care singur ar termina lucrarea într-o oră?

(5p)     5. Un cub este alcătuit din \(125\) cuburi albe şi roşii. Cuburile albe ajung exact, ca feţele cubului să arate ca o tablă de şah. Câte cuburi roşii sunt, dacă în vârfuri sunt cuburile roşii?

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

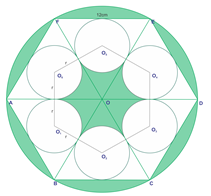
1. Fie hexagonul \(ABCDEF\) (Fig 1.) cu \(AB=12cm\). (Fig.1), \(O\) centru cercului circumscris hexagonului, \({{O}_{i}},i=\overline{1,6}\) centrele cercurilor înscrise in triunghiurile \(AOB,BOC,...,FOA\).

 (5p)  a) Să se demonstreze că \({{O}_{1}}{{O}_{2}}{{O}_{3}}{{O}_{4}}{{O}_{5}}{{O}_{6}}\) este hexagon regulat;

 (5p)  b) Să se calculeze aria \({{A}_{{{O}_{1}}{{O}_{2}}{{O}_{3}}{{O}_{4}}{{O}_{5}}{{O}_{6}}}}\);

 (5p)  c) Să se calculeze raportul dintre aria zonei haşurate din centrul hexagonului si aria zonei haşurate din afara hexagonului.

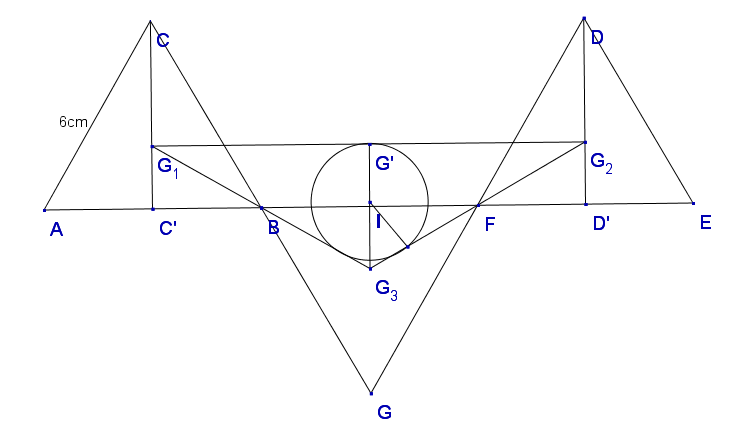
 2. Fie \(ABC\),\(BGF\) şi \(FDE\) trei triunghiuri echilaterale (Fig 2.), congruente, \(AB=BF=FE=6cm\), \({{G}_{1}}\),\({{G}_{2}}\) şi \({{G}_{3}}\)sunt centrele de greutate ale triunghiurilor \(ABC\),\(BGF\) şi \(FDE\).

(5p)  a) Să se calculeze aria\({{A}_{{{G}_{1}}{{G}_{2}}{{G}_{3}}}}\);

(5p)  b) \({{G}_{1}}D=?\)

(5p)  c) Să se calculeze raza cercului înscris în triunghiul \({{G}_{1}}{{G}_{2}}{{G}_{3}}\).