Varianta 128

Prof:Oláh Csaba.

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. În scrierea numărului \(\frac{1}{7}\)sub formă zecimală, pe locul \(100\)după virgulă se află ....

(5p)     2. Dacă \(A=\left\{ \left. x\in R \right|x<\frac{13}{2} \right\}\), atunci \(A\cap N=\left\{ ........ \right.\)

(5p)     3. Numărul cifrelor lui \(n={{8}^{2}}\cdot {{5}^{6}}\) este.......

(5p)     4. Dacă \(\frac{x}{2}=\frac{y}{4}\) şi \(x+y=12\), atunci \(x\cdot y=\).......

(5p)     5. Elevii unei clase schimbă poze între ei. Fiecare dă o poză la fiecare, astfel se împart in total \(240\) de poze. Numărul elevilor din clasă este........

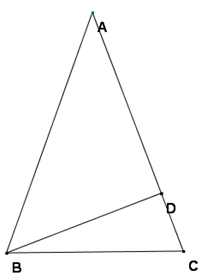
(5p)     6. Se consideră triunghiul \(ABC\)  pe desenul de mai jos - \(AB=AC\), \(BD\bot AC\),

\(m\left( DBC \right)={{25}^{\circ }}\), atunci \(m\left( BAC \right)=...\).....

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Perimetrul unui pătrat a fost crescut cu \(40%\), fiecare latură în mod egal. Cu câte procente a crescut aria pătratului?

(5p)     2. Determinaţi cifrele \(x,y\), dacă \(\overline{24x68y}\vdots 9\).

(5p)     3. Aflaţi raportul \(\frac{b}{a}\), dacă se ştiu următoarele: \(a+b=12\) şi \({{a}^{2}}-{{b}^{2}}=144\).

 4. Fie mulţimile: \(A=\left\{ \left. x\in N \right|\frac{3x}{x+1}\in N \right\}\), \(B=\left\{ \left. x\in N \right|10<{{3}^{x}}<250 \right\}\).

(5p)    a). Determinaţi multimea \(A\);

(5p)    b). Determinaţi mulţimea \(B\).

(5p)     5. Catetele unui triunghi dreptunghic au \(8\), şi, respectiv, \(15\) unităţi. Cât de mare este raza cercului circumscris triunghiului?

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Un tâmplar a crescut preţul scaunelor cu \(30%\). După o vreme s-a răzgândit şi a scăzut preţul cu \(30%\), astfel preţul unui scaun era \(91\) lei.

 (5p)  a). Cât costa un scaun iniţial?

 (5p)  b). Cu cât trebuia să mărească preţul ca după o ieftinire de \(30%\) să obţină preţul iniţial?

 (5p)  c). Cât ar costa un scaun dupa o noua scumpire şi ieftinire de \(30%\)?

 2. Înălţimea unei piramide patrulatere regulate \(VABCD\) este dublul bazei. Dacă baza este de \(2\)cm, aflaţi:

(5p)  a). Cosinusul unghiului dintre planul bazei şi o faţă laterală 

(5p)  b). Distanţa mijlocului bazei de la o faţă opusă, laterală.

(5p)  c). Sinusul unghiului determinat de două apoteme opuse.