Varianta 129

Prof: Oláh Csaba

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Înmulţim un număr întreg cu \(\frac{3}{4}\),  acesta se măreşte cu \(1000\). Numărul este.......

(5p)     2. Rezultatul calculului \(1-\left\{ 2-\left[ 3-\left( 4-5 \right) \right] \right\}\) este........

(5p)     3. Aruncăm cu un zar. Probabilitatea ca numărul aruncat să fie număr prim este........

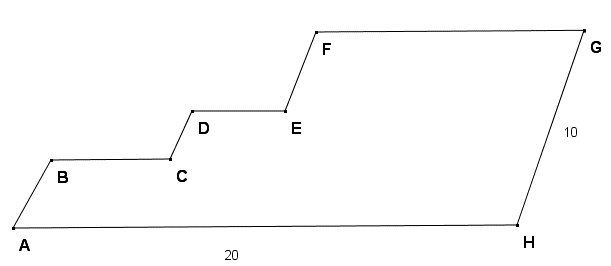
(5p)     4. Dacă \(AH=20\), \(HG=10\), lungimea liniei frânte \(ABCDEFG\) de pe imagine este.....

(5p)     5. Un manual are \(121\) pagini. Pentru paginarea lui s-au folosit .........cifre.

(5p)     6. Dacă \(A\cap B=\left\{ 2,3 \right\}\), \(A\cap C=\left\{ 3,4 \right\}\), atunci \(A\cap \left( B\cup C \right)=\left\{ ... \right.\)

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Determinaţi \(k\in N\), pentru care \(\frac{2k}{3k-1}\in N\).

(5p)     2. În triunghiul \(ABC\), \(m\left( A \right)={{80}^{\circ }}\). Calculaţi măsura unghiului determinat de bisectoarele interioare ale unghiurilor \(B\)şi \(C\).

(5p)     3. Reprezentaţi grafic, într-un singur sistem cartezian, funcţiile: \({{f}_{1}},{{f}_{2}},{{f}_{3}}:R\to R\),

\(f{}_{1}\left( x \right)=x+1\),\({{f}_{2}}\left( x \right)=2x+1\),\({{f}_{3}}\left( x \right)=3x+1\).

 4. \(25%\) din elevii unei clase au părul blond, iar \(75%\)părul şaten. \(50%\) din cei blonzi, şi \(20%\) din cei cu părul şaten, au ochii albaştri.

(5p)    a). Câţi elevi sunt în clasă?

(5p)    b). În procente, câţi elevi din clasă nu au ochii albaştri?

(5p)     5. Descompuneţi în factori: \(\left( a-b \right)\left( {{a}^{2}}-{{c}^{2}} \right)-\left( a-c \right)\left( {{a}^{2}}-{{b}^{2}} \right)\).

            SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Fie funcţiile: \(f,g:R\to R\). Se cunosc următoarele: punctele \(A\left( 1,2 \right),B\left( 0,3 \right)\) aparţin graficului funcţiei \(f\), \(A\left( 1,2 \right)\) aparţine graficului funcţiei \(g\), iar reprezentarea grafică a lui \(g\)este perpendiculară pe graficul lui \(f\).

 (5p)  a). Aflaţi \(f\left( x \right)\);

 (5p)  b). Aflaţi \(g\left( x \right)\);

 (5p)  c). Dacă graficul lui \(g\) trece prin axa \({{O}_{x}}\) in punctul \(C\left( -1,0 \right)\), calculaţi aria triunghiului \(ABC\).

 2. Fie cubul \(\left[ ABCD{A}'{B}'{C}'{D}' \right]\), \(P\) un punct interior cubului. Suma distanţelor lui \(P\) de la feţe este \(9\)cm. Aflaţi:

(5p)  a). Latura cubului;

(5p)  b). Din câte cuburi de volum \(1m{{m}^{3}}\) se poate construi acest cub?

(5p)  c). Aria laterala a piramidei patrulatere regulate înscrise în cub (baza piramidei fiind fata cubului).