Varianta 131

Prof:Oláh Csaba

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.        ( 30 de puncte)

(5p)     1. Suma a \(10\) numere naturale consecutive este \(115\). Ultimul număr din sumă este.....

(5p)     2. Dacă \(x\in R\), \(2\left( x+1 \right):2-2=4\) \(\Rightarrow\) \(x=.....\)

(5p)     3. Numărul pătratelor perfecte de patru cifre, formate din cifrele\(2,3,7,8\) este.........

(5p)     4. Dacă \(\frac{2x+3y}{y}=5\) \(\Rightarrow \)\(\frac{x}{y}=...\)

(5p)     5. În cercul din imagine \(AB=3cm\). Raza cercului are..... cm

(5p)     6. Rezultatul calculului \(0,3+\frac{1}{3}+0,\left( 3 \right)-\frac{3}{10}\) este.........

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Dacă scădem \(18\)dintr-un număr de două cifre, obţinem răsturnatul lui. Aflaţi numărul ştiind că suma cifrelor lui este \(12\).

(5p)     2. Aflaţi aria unui triunghi dreptunghic, dacă o catetă are lungimea de \(6\)cm iar mediana care porneşte din unghiul drept are \(5\)cm.

(5p)     3. Comparaţi numerele: \(3\sqrt{2}\) şi \(\frac{6}{\sqrt{3}}\).

 4. Fie funcţiile \(f:R\to R\), \(f\left( x \right)=\left\{ \begin{align} & 2x-3,x\le 0 \\ & -3x+2,x>0 \\ \end{align} \right.\), \(g:\left( 0,\infty  \right)\to R\), \(g\left( x \right)=2x-3\).

(5p)    a). Reprezentaţi grafic \(f\).

(5p)    b). Rezolvaţi ecuaţia \(f\left( x \right)=g\left( x \right)\).

(5p)     5. Aflaţi raportul \(\frac{{{A}_{AMNCPQ}}}{{{A}_{ABCD}}}\), dacă \(ABCD\)este dreptunghi, iar punctele \(M,N,P,Q\) sunt punctele de mijloc ale laturilor dreptunghiului.

SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Fie sumele:\({{S}_{1}}=\frac{1}{\sqrt{2}+1}+\frac{1}{\sqrt{3}+\sqrt{2}}+\frac{1}{\sqrt{4}+\sqrt{3}}+...\),\({{S}_{2}}=\frac{1-\sqrt{2}}{\sqrt{2}}+\frac{\sqrt{2}-\sqrt{3}}{\sqrt{6}}+\frac{\sqrt{3}-\sqrt{4}}{\sqrt{12}}+...\)

 (5p)  a). Aflaţi valoarea sumei \({{S}_{1}}\) dacă are \(9\) membri;

 (5p)  b). Aflaţi valoarea sumei \({{S}_{2}}\)dacă are \(9\)membri;

 (5p)  c). Câţi membri are\({{S}_{2}}\) dacă \({{S}_{2}}=-\frac{9}{10}\).

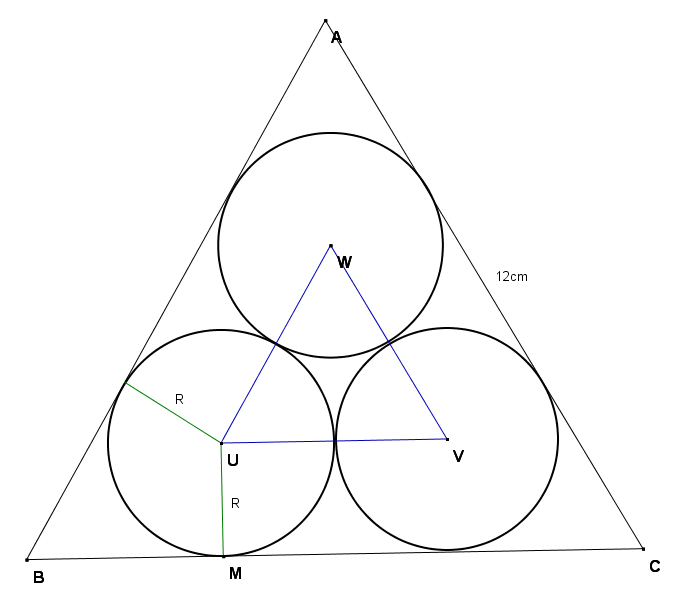
 2. Într-un triunghi echilateral cu lungimea unei laturi de \(12\)cm înscriem trei cercuri cu raze \(R\), după cum arată desenul alăturat. Să calculăm:

(5p)  a). Lungimea razei \(R\);

(5p)  b). Lungimea segmentului \(\left[ BM \right]\), dacă \(R=3\left( \sqrt{3}-1 \right)cm\);

(5p)  c). \(\frac{{{A}_{UVW}}}{{{A}_{ABC}}}=\)?