Varianta 132
Prof: Păcurar Cornel-Cosmin
- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.
- Timpul efectiv de lucru: 2 ore.
SUBIECTUL I – Pe foaia de examen se trec doar rezultatele. ( 30 de puncte)
(5p) 1. Rezultatul calculului \(10-2:2\) este egal cu....
(5p) 2. Numerele întregi din intervalul \(\left[ -6;7 \right]\) sunt în număr de ....
(5p) 3. Patru kilograme de mere costă 10 lei.Trei kilograme de mere de aceeași calitate costă ... lei.
(5p) 4. Un triunghi echilateral are latura de lungime 6m.Aria triunghiului este egală cu... m2
(5p) 5. O prismă dreaptă \(ABC{{A}^{'}}{{B}^{'}}{{C}^{'}}\) are ca baze triunghiurile echilaterale \(ABC\) și \({{A}^{'}}{{B}^{'}}{{C}^{'}}\).
Dacă \(AB=A{{A}^{'}}=3\)m,atunci suma lungimilor tuturor muchiilor prismei este egală cu ... m.
(5p) 6. Numărul elevilor din clasa a VIII-a a unei școli și notele obținute la teza la matematică sunt reprezentate în tabelul de mai jos.
|
Nota obținută |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Număr elevi |
1 |
2 |
3 |
4 |
7 |
5 |
5 |
2 |
Numărul elevilor din clasă este egal cu....
SUBIECTUL II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)
(5p) 1. Desenați, pe foaia de examen, o piramidă patrulateră regulată de vârf V și bază ABCD.
(5p) 2. Media aritmetică a două numere naturale este 10 și unul dintre numere este cu 8 mai mare decât celălalt.Determinați cele două numere.
(5p) 3.Determinați valoarea numărului real \(a\) știind că punctul \(A\left( 3;3a \right)\) aparține graficului funcției \(f:\mathbb{R}\to \mathbb{R},f\left( x \right)=\left( 5-a \right)x+3\).
4. Prețul unui telefon mobil a scăzut cu \(10%\) și,după o săptămână, noul preț a scăzut cu \(15%\).După cele două modificări de preț, telefonul costă 153 lei.
(5p) a) Arătați că prețul inițial al telefonului a fost de 200 de lei.
(5p) b) Cu ce procent din prețul inițial s-a micșorat prețul produsului după cele două ieftiniri?
(5p) 5. Calculați \({{x}^{2}}+\frac{1}{{{x}^{2}}}\), știind că\({{\left( x-\frac{1}{x} \right)}^{2}}=14\), unde \(x\in {{\mathbb{R}}^{*}}\).
SUBIECTUL III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)
1. Laboratorul unei cofetării prepară bomboane în formă de piramidă patrulateră regulată cu toate muchiile egale cu 4 cm.
(5p) a)Arătați că înălțimea piramidei este de \(2\sqrt{2}\) cm.
(5p) b)Calculați volumul unei bomboane.
(5p) c)Fiecare bomboană este acoperită în totalitate cu staniol.Arătați că aria suprafeței minime de staniol necesar împachetării a 100 de bomboane este mai mare decât 4368 cm2 n(se neglijează pierderile la suprapuneri).
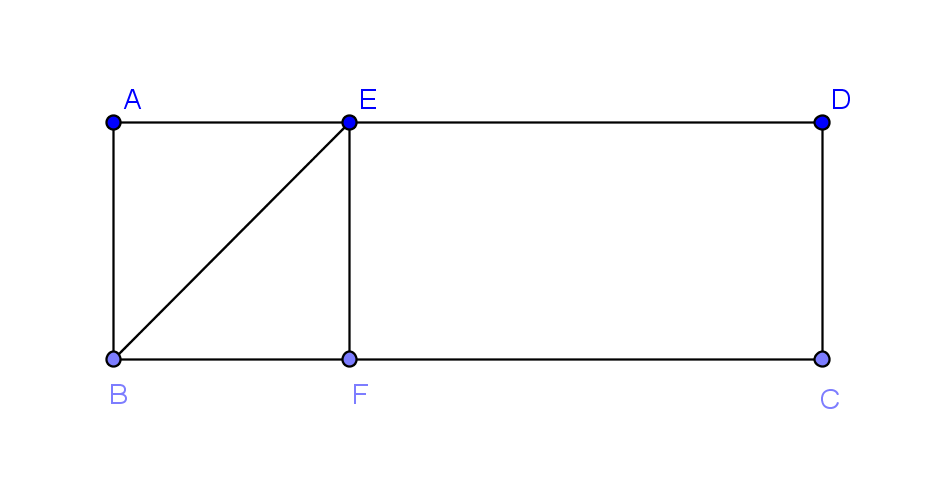
2. Figura de mai jos reprezintă schița unui teren a cărui arie este de 48 hectare.
(5p) a)Exprimați aria terenului în \({{m}^{2}}.\)
Pe acest teren , se sapă un șanț \(\left[ BE \right]\) pentru canalizare \(\left( E\in AD \right)\).Unghiurile ABE și AEB sunt congruente.Valoarea raportului dintre aria triunghiului ABE și aria dreptunghiului ABCD este de \(\frac{1}{6}\).
(5p) b)Arătați că \(BC=3AB\).
(5p) c)Calculați lungimea, exprimată în metri, a șanțului \(\left[ BE \right]\) și aproximați rezultatul cu cel mai apropiat număr natural.