Varianta 135

Prof: Valer Pop

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Dacă 72+48:x=88, atunci x este egal cu ………..

(5p)     2. Pentru o cantitate de fructe un cumpărător plăteşte  132 de lei. Dacă ar fi cumpărat doar un sfert din cantitate, atunci ar fi plătit ................lei.

(5p)     3. Acum o carte costă 64 de lei. Dacă preţul ei se măreşte cu 25%, atunci va costa..........lei .

 (5p)     4. Un dreptunghi are lungimea de 32 cm şi lăţimea de 18 cm. Cât reprezintă \(\frac{5}{16}\) din aria dreptunghiului ?

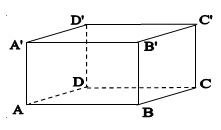
(5p)     5. Se dă paralelipipedul dreptunghic ABCDA’B’C’D’. Măsura unghiului dintre dreptele  CD’ şi AD are măsura de ...............grade. 

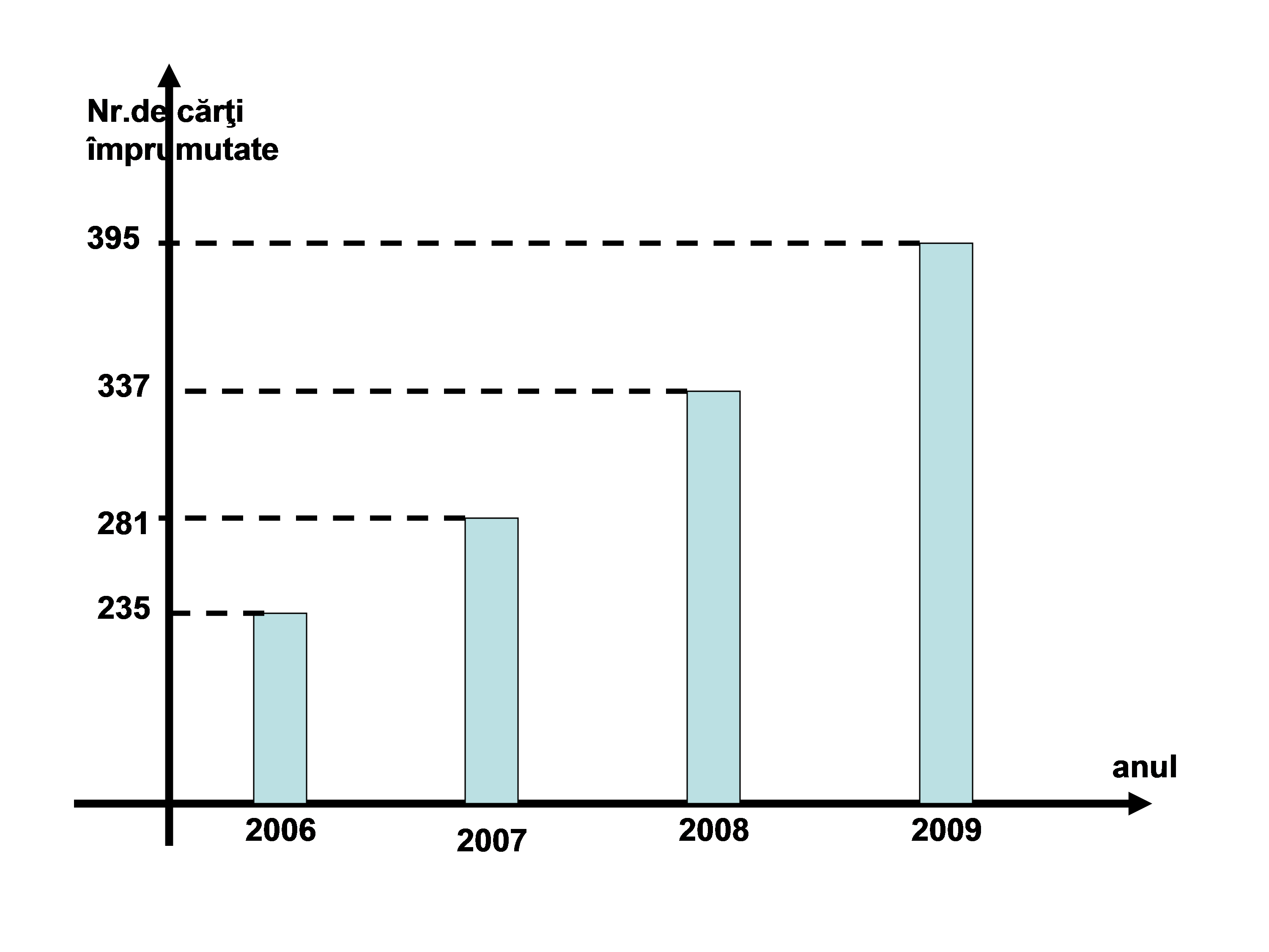
(5p)     6. În graficul de mai jos avem reprezentate numerele care reprezintă cărţile împrumutate de elevii unei şcoli pe durata a patru ani. În ce an au împrumutat elevii un număr de cărţi care este cel mai apropiat de media celor patru ani ?

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi o prismă patrulateră regulată notată ABCDEFGH.

(5p)     2. Se dă mulţimea A={x\(\in \mathbb{N}\)| 1\(\le x-3\)<6}. Enumeraţi elementele mulţimii A∩[2;8).

(5p)     3. Din 5kg de cafea verde se obţin 3,6kg de cafea prăjită. Ce cantitate de cafea verde     este necesară pentru a obţine 12kg de cafea prăjită?

 4. Se dau funcţiile f:\(\mathbb{R}\)\(\to \)\(\mathbb{R}\), f(x)= -x+3 şi g:\(\mathbb{R}\)\(\to \)\(\mathbb{R}\), g(x)=2x-1.

(5p)    a) Aflaţi x\(\in \mathbb{R}\) astfel încât 2f(x)+3=g(x)-2.

(5p)    b) Stabiliţi valoarea de adevăr a propoziţiei: - f(-3)>g(-2).

(5p)     5. Determinaţi numărul x astfel încât numărul \(n={{\left( \text{x}-\text{2} \right)}^{\text{2}}}+{{\left( \text{2x}+\text{1} \right)}^{\text{2}}}-\text{5}\left( \text{x}-\text{2} \right)\left( \text{x}+\text{3} \right)\text{ }\) este natural şi n\(\in (2\sqrt{6};3\sqrt{3})\).

       SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Un siloz pentru depozitarea grâului are forma unui cub cu muchia de 12m , este încărcat 90% din volumul său. Grâul se transportă din depozit cu un camion a cărei ladă are formă de paralelipiped dreptunghic cu dimensiunile de 4m, 2,4m şi 1,2m.

 (5p)  a) Care este numărul minim de transporturi ale camionului pentru a goli silozul?

 (5p)  b) 1m³ de grâu cântăreşte 600kg. Câte tone de grâu sunt la început în siloz?

 (5p)  c) 1kg de grâu se vinde cu 0,45 de lei. Ce sumă se încasează din vânzarea grâului?

 2. În figura de mai jos este schiţa unui teren. Se dă DB=78m, OB=30m.  

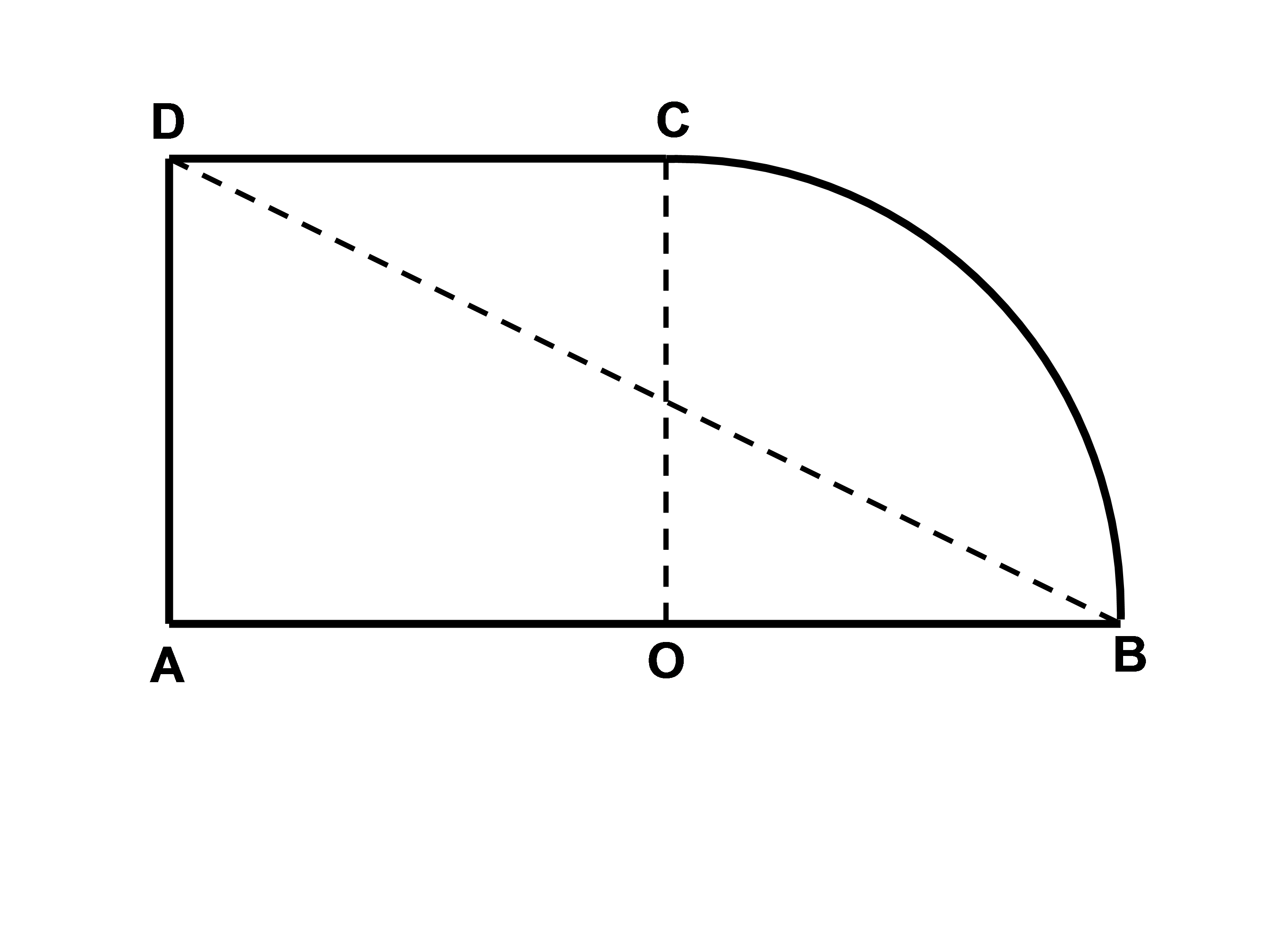
(5p)  a) Calculaţi aria terenului;

(5p)  b) Calculaţi lungimea gardului care împrejmuieşte terenul;

 (5p)  c) Suprafaţa ABD se cultivă cu roşii iar restul din teren cu trandafiri. Calculaţi cu aproximaţie de 1m² prin lipsă, suprafaţa cultivată cu trandafiri.