Varianta 138

Prof: Popa Camelia Sanda

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului 515 : 5- 9² este.......................................

(5p)     2. Soluţia ecuaţiei \(2x+5=-7\)este \(x=\)............................................

(5p)     3. Media geometrică a numerelor \(3-\sqrt{5}\) şi \(3+\sqrt{5}\)este........................

(5p)     4. Linia mijlocie a unui trapez are lungimea de 15 cm iar înălţimea lui are lungimea de 8 cm . Atunci, aria trapezului este .....................................................cm²

(5p)     5. Diagonala unui cub are lungimea de \(4\sqrt{3}\)cm. Atunci suma lungimilor tuturor muchiilor este de .............................................................................cm.

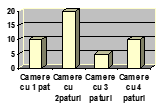
(5p)     6. La o cabană se realizeză  următorul grafic al numărului de locuri.( un pat = un loc)

Câte locuri de cazare are cabana?

SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, o piramidă patrulateră regulată dreaptă MABCD.

(5p)     2. Numerele a şi b sunt direct proporţionale cu 11 respectiv 4 . Dacă împărţim numărul a la numărul b obţinem câtul 2 şi restul 30. Caculaţi numerele a şi b.

(5p)     3. Tatăl şi fiul au împreună 60 de ani . Valoarea raportului vârstelor lor este egală cu 2,75.Cu câţi ani în urmă vârsta tatălui era de trei ori mai mare decât vârsta fiului.

4. Fie funcţia \(f:R\to R,\)\(f\left( x \right)=ax+2a+1,a\in R\)

(5p)    a) Calculaţi valorile reale ale lui \(a\) ştiind că \(f\left( 1 \right)\cdot f\left( -1 \right)-8=0\)

(5p)    b) Pentru \(a=1\), Calculaţi distanţa de la punctul \(M\left( 0,-5 \right)\)la dreapta care reprezintă graficul funcţiei \(f\).

(5p)     5. Arătaţi că \({{\left( x+2 \right)}^{3}}-x-2=\left( x+1 \right)\left( x+2 \right)\left( x+3 \right)\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Un rezervor de apă în formă de cub , este adânc de 2m. Exteriorul lui se vopseşte,folosindu-se 2 litri/m² iar vopseaua este în cutii de 4 litri.

 (5p)  a) Pentru cât timp ar ajunge apa din acest rezervor dacă zilnic s-ar folosi la udarea răsadurilor  250litri de apă , rezervorul fiind, la început, plin?

 (5p)  b) Câte cutii sunt necesare pentru vopsire?

 (5p)  c) Se poate scufunda în bazin o vergea metalică cu lungimea de 3,5m?

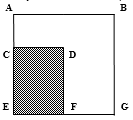
 2. Pătratul ABGE reprezintă o grădină, iar dreptunghiul CDEF, suprafaţa cultivată cu cartofi. Ştiind că EG = 36 m , FG = x m, AC = 16 m

(5p)  a) Exprimaţi, în funcţie de \(x\), suprafaţa pe care nu sunt cultivaţi cartofi.

(5p)  b) Care este valoarea lui \(x\), ştiind că suprafaţa plantată cu cartofi este 30% din suprafaţa totală a terenului?

(5p)  c) Grădina  este împrejmuită  cu un gard de sârmă cu înălţimea de 1,5m. Cât costă gardul, ştiind că un metru pătrat de gard costă 25 lei?