Varianta 139

Prof:Popa Camelia Sanda

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului \(0,001\cdot 1000-{{0}^{4}}\)este .......................................................

(5p)     2. Cel mai mic multiplu comun al numerelor 21 şi 70 este........................................

(5p)     3. Trei ore au un total de ............................................minute

(5p)     4. Un cub are volumul de 1 dm³. Dacă dublăm muchia cubului, atunci volumul cubului va fi egal cu............................................dm³

(5p)     5. Suplementul unui unghi cu măsura de \({{42}^{\circ }}\) are măsura de .....................\(^{\circ }\)

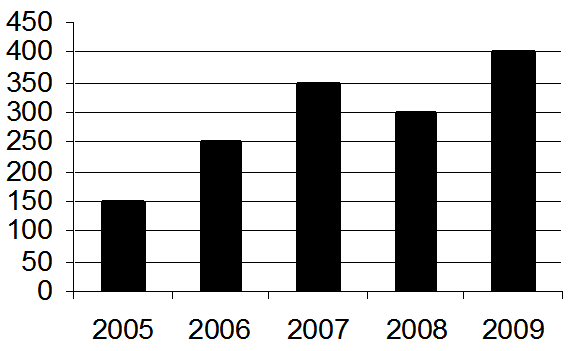
(5p)     6. Diagrama reprezintă numărul de cărţi împrumutate de la o bibliotecă şcolară în ultimii 5 ani .Care a fost numărul mediu de cărţi împrumutate în primii trei ani?

   SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen,  o prismă patrulateră regulată ABCDEFGH.

(5p)     2. Diferenţa a două numere naturale este 120. Dintre cele două numere, cel mai mare este divizibil cu 10, iar cel mai mic este divizibil cu 6. Câtul împărţirii celui mai mare la 5 este cu 20 mai mare decât câtul împărţirii celui mai mic la 3 . Aflaţi numerele.

(5p)     3. Într-un parc zoologic vizita costă 25 de lei pentru un adult şi 10 lei pentru un copil. La sfârşitul unei zile s-a constatat că 630 de persoane au vizitat parcul zoologic, iar suma încasată a fost de 9525 de lei. Aflaţi numărul adulţilor care au vizitat parcul în ziua respectivă.

4. Se consideră expresiile \({{E}_{1}}\left( x \right)=\frac{x+3}{{{x}^{2}}+6x+9},x\in R-\left\{ -3 \right\}\) şi \({{E}_{2}}\left( x \right)=\frac{x-1}{x+3}+\frac{x+2}{x-3}-\frac{7x+9}{{{x}^{2}}-9},x\in R-\left\{ \pm 3 \right\}\).

(5p)    a) Simplificaţi prin\(x+3\)expresia \({{E}_{1}}\left( x \right)\).

(5p)    b) Determinaţi \(x\in \mathbb{Z}-\left\{ 0 \right\}\) atfel încât \(\frac{1}{2}{{E}_{2}}\left( x \right)\in \mathbb{Z}\)

(5p)     5. Fie funcţia \(f:R\to R,f\left( x \right)=2x-1\). Determinaţi numerele reale\(a\)pentru care punctul  \(C\left( {{a}^{2}};3a+1 \right)\) aparţine graficului funcţiei.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. În figura alăturată este reprezentat schematic un

rezervor de apă . VABCD este o piramidă patrulateră regulată dreaptă cu AB = 2 m, unghiul diedru al planelor (VAD) şi (VBC) este de 60°, ABCDA`B`C`D`este o prismă patrulateră regulată dreaptă cu CC` = 0,5 m.

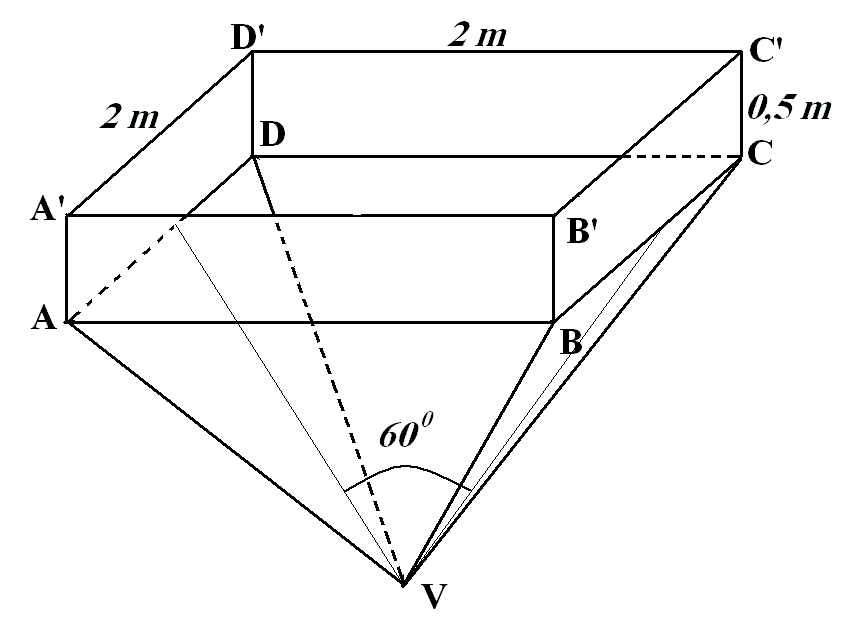
 (5p)  a) Să se calculeze volumul prismei ABCDA`B`C`D`  .

 (5p)  b) Calculaţi aria laterală a piramidei VABCD.

 (5p)  c) Dacă golirea rezervorului se face cu ajutorul a 4 robinete care au debitul de 5\(l\) /minut fiecare , în cât timp se va goli rezervorul?    

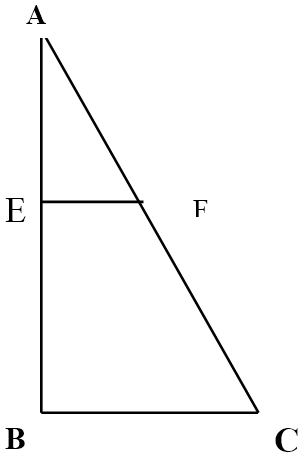
2. În figura de mai jos este reprezentată schematic suprafaţa unui teren agricol.Suprafaţa AEF va fi cultivată cu grâu iar suprafaţa EFCB cu porumb. AB=400m, BC=300m şi AE=\(x\) m (0<x<400).

 (5p)  a) Exprimaţi în funcţie de \(x\), aria suprafeţei AEF.

 (5p)  b) Pentru ce valoare reală a lui x aria suprafeţei AEFeste o treime din aria suprafeţei EFCB ?

 (5p)  c) Se consideră AE= 200 m. Pentru a cultiva această suprafaţă cu grâu trebuie să cumpere sămânţă pentru semănat. 1 kg de sămânţă costă 6 lei.. Cât a costat în total sămânţa ştiind că pentru 1 ha ( 1 ha = 10.000 m²) sunt necesare 15 kg de sămânţă şi se acordă o reducere de 20% din valoarea totală?