Varianta 140

Prof:Popa Camelia Sanda

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului 147 : 7 - 16 este...............................................

(5p)     2. Din cei 25 de elevi ai unei clase 40% studiază limba engleză. Numărul elevilor care studiază limba engleză este...................................................................

(5p)     3. Într-o urnă sunt 17 bile albe şi 13 bile negre. Se extrage o bilă. Probabilitatea ca bila extrasă să fie neagră este..............................................................................

(5p)     4. Un triunghi dreptunghic are o catetă de lungime 15m şi ipotenuza de lungime 17m. Perimetrul triunghiului este de ...................................................m

(5p)     5. Într-un cub \(ABCD{A}'{B}'{C}'{D}'\)lungimea segmentului \({A}'{C}'\)este de 2 cm. Aria triunghiului \({A}'B{C}'\)este egală cu..........................................cm²

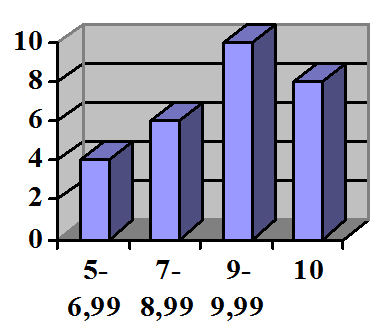
(5p)     6. În graficul din figura alăturată  este prezentată situaţia mediilor generale la clasa a VIII-a A. Numărul elevilor care au media generală cuprinsă între 7 şi 10 este .........................

  SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, o prismă triunghiulară regulată dreaptă \(ABC{A}'{B}'{C}'\).

(5p)     2. Numerele 2168 şi 2039, împărţite la acelaşi număr natural dau resturile 23 şi respectiv 37. Să se afle numărul la care s-a făcut împărţirea .

(5p)     3. Considerăm numerele \(\overline{ab}\) scrise în baza 10 cu \(a\ne 0\)şi \(b\ne 0\), care îndeplinesc condiţia \(\overline{ab}-\overline{ba}=a\cdot b-a\). Determinaţi toate numerele \(\overline{ab}\)care îndeplinesc condiţia dată.

4. Considerăm funcţia \(f:R\to R,f\left( x \right)=2ax-3a+1\), unde \(a\)este un număr real.

(5p)    a) Rezolvaţi în mulţimea numerelor reale ecuaţia \(f\left( a \right)=0\).

(5p)    b) Pentru  \(a=1\), reprezentaţi grafic funcţia f , într-un sistem de axe ortogonale.

(5p)     5. Fie expresia \(E\left( x \right)\)\(=\frac{{{\left( x+2 \right)}^{3}}-x-2}{x\left( x+5 \right)+6},x\in R-\left\{ -2;-3 \right\}\). Arătaţi că pentru orice număr \(n\in N\), \(E\left( n \right)\in N\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Elevii unei şcoli sapă într un parc gropi de forma prismă patrulateră regulată, \(ABCD{A}'{B}'{C}'{D}'\), pentru a planta puieţi  Adâncimea unei gropi este de 75 cm şi baza este un pătrat cu latura de 60cm.

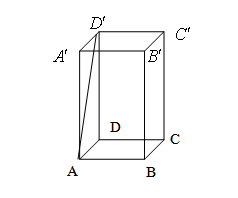
(5p)  a) Calculaţi aria totală  a prismei \(ABCD{A}'{B}'{C}'{D}'\).

 (5p)  b) Calculaţi sinusul unghiului dintre AD’ şi planul bazei

 (5p)  c) Ştiind că elevii au plantat 200 de puieţi, calculaţi ce volum de pământ a fost săpat (în \({{m}^{3}}\))

2. O hală dreptunghiulară se pardoseşte cu pietre în formă de pătrat cu latura de 15 cm. Hala este lungă de 30 m şi lată de 15 m. Între pietre nu rămâne loc liber, iar dacă dintr-o piatră se foloseşte o parte, restul nu se mai foloseşte.

 (5p)  a) Câte pietre sunt necesare?

(5p)  b) Dacă piatra este groasă de 3 cm, ce volum de piatră s-a cumpărat?

(5p)  c) Cât a costat piatra, ştiind că 1m³ costă 20 lei iar pentru cantităţi mai mari de 5 m³ se acordă o reducere de 15% din valoarea totală.