Varianta 145

Prof: RICU ILEANA

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(\sqrt{1-\frac{9}{25}}:\sqrt{0,36}\) este ,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,

(5p)     2. Cel mai mic număr de cinci cifre care are toate cifrele diferite şi este divizibil cu numărul 6 este..................................

(5p)     3. Diana face o prăjitură; dacă consumă patru ouă are nevoie de 280 g de zahăr.

Dacă ar pune trei ouă, atunci ii trebuie...........................g de zahăr.

(5p)     4. Fie ABCD un trapez în care AB║CD, AB = 42, BC = 32, CD = 14 şi AD = 12.                  

      Dacă AD\(\cap \)BC= = {O} , calculaţi OC .

(5p)     5. Un pătrat are acelaşi perimetru cu al unui dreptunghi cu dimensiunile 12 cm şi 6 cm. Aria pătratului este...................................

(5p)     6. 8 elevi trebuie sa citeasca capitolele unui proiect. In tabelul de mai jos este reprezentat modul in care au impartit capitolele:

Numarul mediu de capitole citite de un singur elev este..................................................

 SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi pe foaia de examen piramida triunghiulară regulata VABC.

(5p)     2. Calculati a²+b² stiind ca а + b = 5, iar а ∙ b =\(\frac{1}{4}\)

(5p)     3. Intr-o cutie sunt de cinci ori mai multe bile roşii decât galbene. Dacă se scot 5 bile roşii şi se adaugă o bilă galbenă atunci în cutie sunt de 4 ori mai multe bile roşii decâtgalbene. Câte bile de fiecare culoare au fost la început ?

4. Se consideră functiile \(f:\mathbb{R}\to \mathbb{R},f\left( x \right)=2x-3\) si \(g:\mathbb{R}\to \mathbb{R},g\left( x \right)=-x+6\)

(5p)    a) Reprezentaţi grafic funcţia f în sistemul de coordonate xOy.

(5p)    b) Calculaţi aria triunghiului determinat de reprezentările grafice ale celor două funcţii si axa Ox .

(5p)     5. Numerele a, b şi c sunt direct proporţionale cu 2, 3, şi 4, iar numerele b şi d sunt invers proporţionale cu 2 şi 9.Să se arate că 2a² + b² + 3c² + 10d² este pătratul unui număr .

          SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

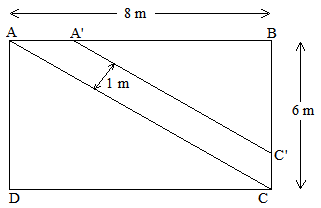
1. Figura alaturată reprezintă schiţa unei grădini dreptunghiulare ABCD si a aleii din interiorul ei. Se stie că AB = 8 m, BC = 6 m, iar lăţimea aleii \(A{A}'{C}'C\)este de 1m .

5p a) Segmentele \(A{A}'\) si \({C}'C\)reprezintă porţi de acces în grădină. Se împrejmuieste grădina cu gard, nu si în dreptul porţilor. Calculaţi lungimea gardului exterior care înconjoară grădina.

5p b) Calculaţi aria suprafeţei ocupată de alee.

5p c) În interiorul celor doua parcele formate \({A}'B{C}'\) şi \(ADC\)se amenajează câte un strat cu flori, în formă de cerc. Calculaţi aria maximă a unui astfel de strat.

2.Un bazin de înotîn formă de paralelipiped dreptunghic are lungimea de 24m,lăţimea de 10m şi înălţimea de 2,5m.

(5p)  a) Câţi metri pătraţi de faianţă sunt necesari pentru faianţarea pereţilor şi fundului bazinului?

(5p)  b) Câţi litri de apă sunt necesari pentru a umple 80% din bazin şi care sunt costurile pe lună, ştiind că pentru 1000 litri se consumă 1kWh energie electrică al cărui preţ este de 0,35lei/kWh ,iar apa se înlocuieşte de 4 ori pe lună?

(5p)  c) Până la ce înălţime se ridică apa în bazin,ştiind că se toarnă 480000 litri de apă?