Varianta 146

Prof: RICU ILEANA

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)    1. Rezultatul calculului \({{222}^{10}}-{{4}^{5}}\cdot {{111}^{10}}+{{2}^{2}}\cdot \left( 2+2\cdot 3 \right)\) este: ..............................

(5p)    2. Media geometrică a numerelor 6²:3²+7 şi \(x\) este 22. Numărul raţional pozitiv \(x\) este egal cu .............................................

(5p)    3. Probabilitatea ca aruncând două zaruri să obţinem două feţe în care suma punctelor să fie un număr prim este.............................................

(5p)     4. Un ceas indică ora 14 şi 30 minute. Măsura unghiului format de acul orar şi cel minutar este.......................................

(5p)     5, Volumul unui cub este 5,832 dm³.Muchia cubului este .............................cm.

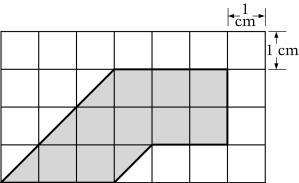
(5p)     6. Aria suprafetei hasurate din figura alăturată este de ..............................cm² .

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p) 1. Desenati  o prisma patrulatera dreapta ABCDA′B′C′D′.

(5p) 2. Ştiind că ac - bc + 3c = 3293 şi c = 89, unde a,b,c\(\in N\), calculati numărul a - b .

(5p) 3. Raportul dintre complementul şi suplementul unui unghi este\(\frac{1}{19}\).Aflaţi măsura unghiului.

4. Se consideră functia \(f:\mathbb{R}\to \mathbb{R},f\left( x \right)=3-4x\)

(5p)    a) Reprezentaţi grafic funcţia f  în sistemul de coordonate xOy.

(5p)    b)Sa se determine solutiile naturale ale inecuatiei

(5p) 5. Calculati valoarea expresiei \(4{{x}^{2}}+{{y}^{2}}\),stiind ca 2x-y=4  si \(x+\frac{y}{2}=1\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

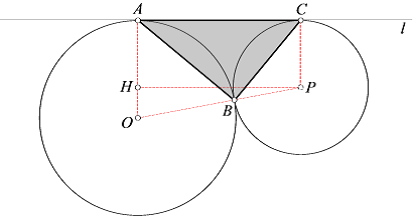
  1.În figura de mai jos se dau două cercuri tangente exterioare cu razele de 9cm şi 3cm şi una din tangentele lor exterioare.

 (5p)  a) Justificaţi că patrulaterul OACP este trapez dreptunghic şi arătaţi că aria acestuia este de \(36\sqrt{3}c{{m}^{2}}\).

(5p)  b) Calculaţi aria \(\vartriangle ABC\).

 (5p)  c) Determinaţi aria suprafeţei cuprinsă între cele două cercuri şi tangenta l  exterioară comună.

2*. Pentru un spectacol de circ desfăşurat în aer liber se improvizează un cort în formă de piramidă hexagonală regulată VABCDEF având muchiile laterale de 13 m şi latura bazei de 10 m.

(5p)  a) Să se afle înălţimea şi apotema piramidei.

(5p)  b) Calculaţi volumul piramidei date şi arătaţi că aria laterală este de 360 m².

(5p)  c) Se ştie că suprafaţa laterală se acoperă cu strat dublu de foaie de cort care costă 13,50 lei/m²,iar suprafata bazei se acoperă cu scândură pentru care se plăteşte 20lei/m².

Calculaţi costurile realizării cortului improvizat.