Varianta 147

Prof: Ricu Ileana

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.         

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului : −| 3 | + | − 2| − 2²+ (−1)³ este   ………………….

(5p)     2. Valoarea lui x din proporţia \(\frac{x}{\sqrt{4+2\sqrt{3}}}=\frac{\sqrt{4-2\sqrt{3}}}{5-\sqrt{3}}\)este………………………

(5p)     3. Se consideră ecuaţia x²+6=5x. Probabilitatea ca,alegând un număr oarecare din mulţimea A={x\(\in \)N/1<x<6}, acesta să fie soluţie a ecuaţiei date este……………………………….

(5p)     4. Un obiect costă 50 lei. Preţul obiectului după o scumpire cu 40% şi apoi o reducere cu 40% este....................................

(5p)     5. Într-un triunghi ABC dreptunghic în A, AD\(\bot \)BC, AD=12cm, CD=8cm.

Atunci aria triunghiului ABC este egală cu ..................................

(5p)     6. Un post de televiziune a efectuat un sondaj asupra a 2000 de indivizi referitoare la percepţia acestora la relatările postului TV. Rezultatele în procentaje sunt prezentate in tabelul urmator.Stabiliţi câte persoane cu vârsta între [35;55) ani urmăresc emisiunile TV.

   SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Suma a trei numere naturale este de 200. Suma primelor două numere este egală cu al treilea număr, iar diferenţa lor este de 10.  Aflaţi numerele

(5p)     2. O prismă dreaptă are aria bazei de 25 cm² iar volumul de 200 cm³. Calculaţi înălţimea prismei.

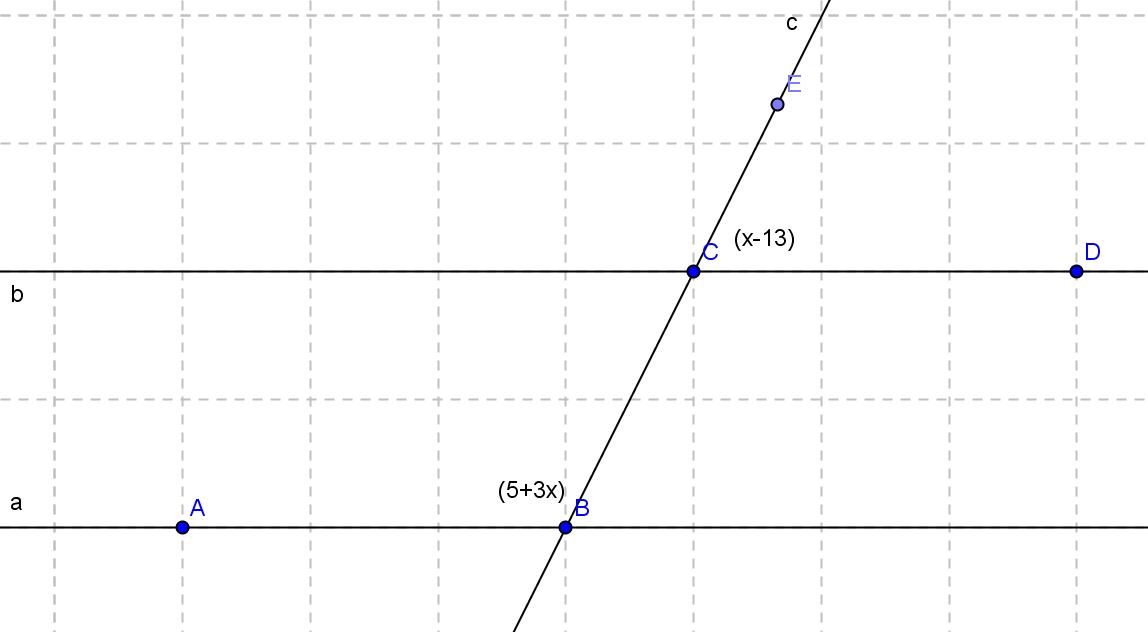
(5p)     3. Dreptele paralele a şi b sunt intersectate de secanta c formând unghiurile marcate în figura de mai jos cu \(m\left( \sphericalangle DCE \right)={{\left( x-13 \right)}^{\circ }}\)şi \(m\left( \sphericalangle ABC \right)={{\left( 5+3x \right)}^{\circ }}\).Calculaţi valoarea lui x .

4. Fie expresia \(E\left( x \right)=2\left[ \left( \frac{x}{x+1}-\frac{{{x}^{2}}}{{{x}^{2}}+2x+1} \right):\left( \frac{x}{{{x}^{2}}-1}-\frac{1}{x+1} \right) \right]\)

(5p)    a)Arătaţi că \(E\left( x \right)=\frac{2x\left( x-1 \right)}{x+1}\)

(5p)    b)Calculaţi \(E\left( \sqrt{2} \right)+8\)

SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Se considera cubul ABCDA^/B^/C^/D^/ cu  AB = 12 cm;notam cu  O^/ centrul feţei A^/B^/C^/D^/ .              

(5p)  a). Calculaţi lungimea segmentului O^/B;                                            

(5p)  b). Aflaţi măsura unghiului dintre dreptele AD^/  şi A^/B;                       

(5p)  c). Arătaţi că DB^/ perpendicular (AD^/C)

2*. Se consideră o prismă patrulateră regulată dreaptă cu muchia bazei de 7cm şi înălţimea de 2 dm in care se strunjeşte o gaură cilindrică cu diametrul de 6cm şi înălţimea de 1,5dm în care se toarnă plumb (densitatea plumbului este 11,3 g/ cm³). Aflaţi:

 (5p)  a)Volumul prismei date

 (5p) b)Volumul cilindrului obţinut prin strunjire

 (5p)  c)Câte kg de  plumb topit se toarnă în gaura cilindrică pentru realizarea unei piese.