Varianta 149

Prof: Ricu Ileana

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Fie mulţimea A={\(\left\{ -2,3\left( 6 \right);-3\sqrt{2};\sqrt{9};\pi ;2\frac{1}{2};\sqrt{6\frac{1}{4}};0,25 \right\}\).

Mulţimea\(A\cap \left( \mathbb{R}\backslash \mathbb{Q} \right)\)este…………………………………….

(5p)    2. Mulţimea soluţiilor ecuaţiei \(\sqrt{{{\left( x-1 \right)}^{2}}}=4\) este ………………………

(5p)     3. Un paralelipiped dreptunghic are dimensiunile de 3 cm, 4 cm şi 12 cm. Diagonala lui este de ……………. cm.

(5p)    4. Se consideră arcul de cerc QR din cercul de centru P şi rază r;coarda QR are lungimea egală cu raza cercului. Măsura unghiului PRQ este……………………

(5p)     5. Care este probabilitatea ca,scriind un număr oarecare de trei cifre,acesta să fie multiplu de 47 ?

(5p)     6. Proiectul de buget al unei ţări pentru anul 2011 distribuie cele 280 miliarde euro conform datelor din tabelul de mai jos.Stabiliţi bugetul propus pentru ministerul apărării.

SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Numărătorul unei fracţii \(\frac{a}{b}\) este cu 8 mai mic decât numitorul. Mărind pe a cu 5 şi micşorând pe b cu 1, fracţia astfel obţinută este 0,(8). Determinaţi fracţia.

(5p)    2. Un dreptunghi are aria egală cu 800\(c{{m}^{2}}\).Calculaţi aria acestuia ştiind că cele două dimensiuni se măresc cu 25%.                                                   

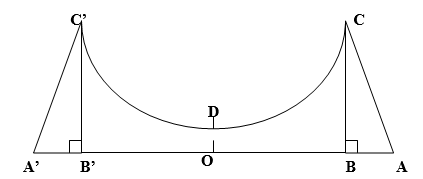
(5p)      3. Figura de mai jos reprezintă o secţiune longitudinală a unei piste de skate-board;ştiind că OB = 4 m ; OD = 0,5 m ; BC = 4,5 m , OD este axa de simetrie a figurii,iar lărgimea pistei este de 5m,calculaţi aria pistei. OD=Axa de simetrie

4. Se consideră expresia \(E\left( x \right)=\frac{1}{\sqrt{x}-\sqrt{1-x}}-\frac{1}{\sqrt{x}+\sqrt{1-x}},x\in \left[ 0;1 \right]\backslash \left\{ \frac{1}{2} \right\}\)

(5p)    a)Calculaţi valoarea lui E pentru \(x=2\sqrt{3}-3\)

(5p)    b)Să se rezolve ecuaţia E(x)=2

(5p)    5. Un paralelogram ABCD cu \(m\left( \angle DAB \right)={{30}^{0}}\)are perimetrul de 30cm, iar AD este jumătate din AB. Calculaţi aria paralelogramului .   

SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Fie ABCD un dreptunghi cu AB=27cm,DA=48cm.În vârful A se ridică perpendiculara AM pe planul acestuia astfel încât AM=36cm . Notăm cu O mijlocul segmentului [MC].Calculaţi:

(5p)  a)Distanţa de la punctual O la dreapta CD.

(5p)  b)Valoarea expresiei \(\sin \left( \sphericalangle ADM \right)+3\cos \left( \sphericalangle ABM \right)+4tg\left( \sphericalangle ADB \right)\)

(5p)  c)Lungimea proiecţiei segmentului [CM] pe planul (ADM)

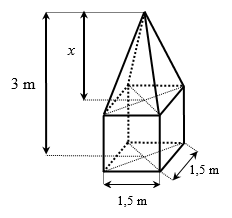
2. Un artist plastic trebuie să sculpteze un monument având forma şi dimensiunile din figura de mai jos(o piramidă patrulateră regulată suprapusă unui cub). Calculaţi:

(5p)  a) Volumul monumentului realizat.

 (5p)  b) Suprafaţa monumentului.

 (5p)  c)Calculaţi masa monumentului ştiind că densitatea materialului din care este realizat este de \(\rho \)=1,5 kg/dm³(\(\rho =\frac{m}{V}\))